3．顶点

抛物线和它的轴的交点叫做抛物线的顶点．在方程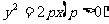中，当y=0时，x=0，因此抛物线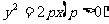的顶点就是坐标原点．

2．对称性

以－y代y，方程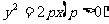不变，所以这条抛物线关于x轴对称，我们把抛物线的对称轴叫做抛物线的轴．

1．范围

因为p＞0，由方程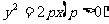可知，这条抛物线上的点M的坐标(x，y)满足不等式x≥0，所以这条抛物线在y轴的右侧；当x的值增大时，|y|也增大，这说明抛物线向右上方和右下方无限延伸．

例1 (1)已知抛物线标准方程是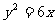，则它的焦点坐标为，

准线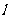的方程为

　解：(1)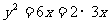

p＝3，焦点坐标是(，0)准线方程是x＝－．

即学即练1

(2)已知抛物线的焦点坐标是F(2，0)，求它的标准方程是

解：焦点在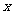轴的正半轴上，设抛物线标准方程是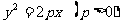

因为焦点坐标是F(2，0)

所以＝2，

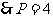
所求抛物线的标准方程是．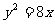

即学即练2

(3) 已知抛物线的准线方程是x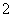＝－,则它的标准方程是.

解：因为抛物线的准线方程是x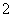＝－,所以焦点在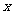轴的正半轴上，

设抛物线标准方程是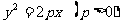

所以＝2，

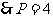
所求抛物线的标准方程是．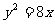

即学即练3

(4) 已知抛物线的焦点在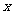轴的正半轴上，经过点P(2,4), 则它的标准方程是.

解：焦点在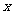轴的正半轴上，设抛物线标准方程是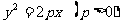

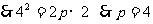
所求抛物线的标准方程是．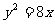

深化思维

(5)点M与点F(4,0)的距离比它到直线的距离小1，求点M的轨迹方程

解法一：可知原条件M点到F(4，0)和到x＝－4距离相等，由抛物线的定义，点M的轨迹是以F(4，0)为焦点，x＝－4为准线的抛物线．

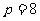
∴所求方程是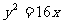

解法二:用直接法求点M的轨迹方程

评价反思 (1)你想到几种解法,哪种简单?

　　　　 　(2) 你体会到数学的等价转换吗?

(3)以上5个小题从定义, 方程,焦点, 准线,图象等方面反映了抛物线的内在联系.

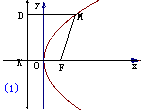
(三) 探究抛物线的标准方程

如图所示，取经过点F且垂直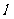的直线为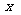轴，垂足为K。以FK的中点O为原点，建立直角坐标系系，设|KF|=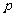(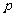>0),

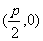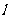那么焦点F的坐标为，准线的方程为，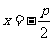

设抛物线上的点M(x,y)，动点M满足的几何条件是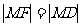

则有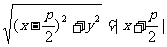

化简方程得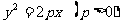

方程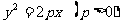叫做抛物线的标准方程

它表示的抛物线的焦点在x轴的正半轴上，焦点坐标是F(,0)，它的准线方程是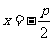

(二) 抛物线的定义

1.定义:平面内与一个定点F和一条不经过定点F的定直线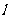的距离相等的点的轨迹

叫做抛物线

定点F叫做抛物线的焦点，定直线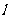叫做抛物线的准线

2. 定义深化:

(1) 定直线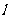不经过定点F

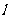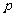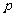　(2) 定点F到定直线的距离记为(>0)

3.注意两个距离相等,可互相转换

(一)探究抛物线的定义

动画演示抛物线的形成过程

学生探究P64探究

(1)平面内一个定点F和一条不经过定点F的定直线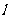

(2)在直线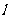上任取点H，过点H作

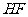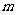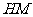(3)作线段的垂直平分线，交于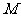

(4)当点H在直线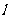上运动时，总有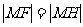，即动点M到定点F的距离和到定直线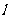的距离相等

(5)动点M的轨迹是一条抛物线

2.生活中的抛物线实例(课件展示)

赵州桥,汽车前灯，太阳灶

1.函数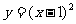的图象是一条,它的对称轴方程是.

抛物线，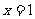

8．相距1400m的A,B两个哨所，听到炮弹爆炸的时间相差3s，已知声音的速度是340m/s,问炮弹爆炸点在怎样的曲线上？