(一)探究抛物线的定义

动画演示抛物线的形成过程

学生探究P64探究：请按下列要求填空

(1)在平面内画一个定点F和一条不经过定点F的定直线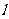

(2)在直线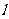上任取点H，过点H作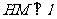

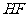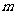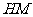(3)作线段的垂直平分线，交于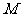

思考：

(4)当点H在直线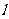上运动时，总有，即动点M到定点F的距离和到定直线的距离

(5)动点M的轨迹是一条

2.生活中的抛物线实例(课件展示)：赵州桥,汽车前灯，太阳灶

1.函数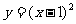的图象是一条,它的对称轴方程是.

4. 你对老师的教学有哪些想法,请告诉老师.

3. 你还有哪些地方不清楚的,请告诉老师.

2.你在哪些数学能力上有所提高?

1.你认为有哪些主要的知识点? 你认为这节课的重点是什么?

P73　　　 2，3，5

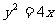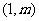例2 (1) 抛物线上一点P 到焦点F的距离是

解: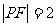

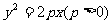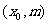　(2) 抛物线上一点P到焦点F的距离是

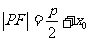
规纳总结：

定义：抛物线上任意一点M与抛物线焦点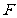的连线段，叫做抛物线的焦半径

抛物线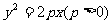焦半径公式是：

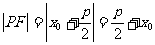
(3)斜率为1的直线经过抛物线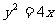的焦点，与抛物线相交于两点A、B，

求线段AB的长

分析：利用根与系数关系及抛物线的定义来解之

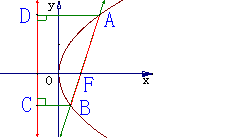解：如图，由抛物线的标准方程可知，抛物线焦点的坐标为F(1，0)， 　　　　　　　　　　　　　　　　所以直线AB的方程为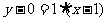

即 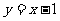　　　　　①

将方程①代入抛物线方程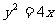，得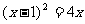　

化简得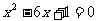

由抛物线的定义可知，|AF|等于点A到准线x=－1的距离|AD|，而|AD|=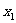+1．同理|BF|＝|BC|=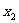+1，于是得

|AB|=|AF+|BF|=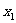++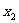2．

根据根与系数的关系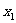+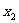＝6．

|AB|=6+2=8．

规纳总结：抛物线的焦点弦长公式|AB|=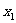++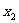P

引申探究

(4) 经过抛物线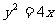的焦点的弦AB的长|AB|=8,求直线AB的方程

(5)经过抛物线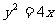的焦点的弦AB，求弦AB的长的最小值

(6) 求经过抛物线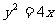的焦点的弦AB的中点的轨迹方程

(7)已知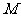为抛物线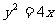上一动点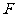，为抛物线的焦点，定点，则的最小值为( 　)

(A)3　　　　　　 (B)4　　　　　　　 (C)5　　　　　　 (D)6

4．离心率

抛物线上的点M与焦点的距离和它到准线的距离的比，叫做抛物线的离心率，用e表示．

由抛物线的定义可知，e=1．

请与椭圆,双曲线的离心率的范围比较:

椭圆的离心率的范围是

双曲线的离心率的范围是