1.你认为有哪些主要的知识点? 你认为这节课的重点是什么?

P73　　　 2，3，5

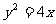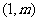例2 (1) 抛物线上一点P 到焦点F的距离是

类比:

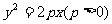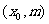(2) 抛物线上一点P到焦点F的距离是

规纳总结：

定义：抛物线上任意一点M与抛物线焦点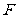的连线段，叫做抛物线的焦半径

抛物线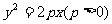焦半径公式是：

(3)斜率为1的直线经过抛物线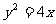的焦点，与抛物线相交于两点A、B，求线段AB的长

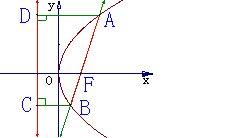
规纳总结：抛物线的焦点弦长公式|AB|=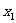++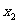P

引申探究

(4) 经过抛物线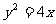的焦点的弦AB的长|AB|=8,求直线AB的方程

(5)经过抛物线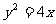的焦点的弦AB，求弦AB的长的最小值

(6) 求经过抛物线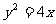的焦点的弦AB的中点的轨迹方程

(7)已知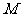为抛物线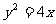上一动点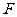，为抛物线的焦点，定点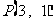，则的最小值为( 　)

(A)3　　　　　　 (B)4　　　　　　　 (C)5　　　　　　 (D)6

4．离心率

抛物线上的点M与焦点的距离和它到准线的距离的比，叫做抛物线的离心率，用e表示．

由抛物线的定义可知，e=．

请与椭圆,双曲线的离心率的范围比较:

椭圆的离心率的范围是

双曲线的离心率的范围是

3．顶点

抛物线和它的轴的交点叫做抛物线的顶点．在方程中，当y=0时，x=0，

因此抛物线的顶点就是．

2．对称性

以－y代y，方程不变，所以这条抛物线关于对称，

我们把抛物线的对称轴叫做抛物线的轴．

1．范围

因为p＞0，由方程可知，这条抛物线上的点M的坐标(x，y)满足不等式x≥0，所以这条抛物线在y轴的；

当x的值增大时，|y|也增大，这说明抛物线向右上方和右下方无限延伸．

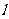例1 (1)已知抛物线标准方程是，则它的焦点坐标为，准线的方程为

即学即练1

(2)已知抛物线的焦点坐标是F(2，0)，求它的标准方程是

即学即练2

(3) 已知抛物线的准线方程是x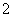＝－,则它的标准方程是.

即学即练3

(4) 已知抛物线的焦点在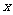轴的正半轴上，经过点P(2,4), 则它的标准方程是.

深化思维

(5)点M与点F(4,0)的距离比它到直线的距离小1，求点M的轨迹方程

评价反思 (1)你想到几种解法,哪种简单?

　　　 　(2) 你体会到数学的等价转换吗?

　　　　 (3)以上5个小题从定义, 方程,焦点, 准线,图象等方面反映了抛物线的内在联系.

(三) 探究抛物线的标准方程

请填空

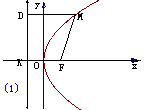如图所示，取经过点F且垂直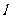的直线为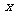轴，垂足为K。以FK的中点O为原点，建立直角坐标系系，设|KF|=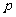(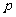>0),

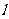那么焦点F的坐标为，准线的方程为，

动点M满足的几何条件是

设抛物线上的点M(x,y)，则有

化简方程得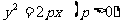

方程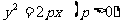叫做抛物线的标准方程

它表示的抛物线的焦点在x轴的正半轴上，焦点坐标是F(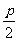,0)，它的准线方程是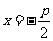

(二) 抛物线的定义

1.定义:平面内与一个定点F和一条不经过定点F的定直线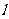的距离的点的轨迹叫做抛物线

定点F叫做抛物线的，定直线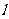叫做抛物线的

2. 定义深化:

(1) 定直线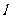不经过定点F

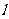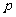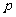　(2) 定点F到定直线的距离记为(>0)

3.注意两个距离相等,可互相转换