
1、范围
因为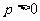 ,由方程
,由方程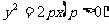 可知,这条抛物线上的点
可知,这条抛物线上的点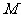 的坐标
的坐标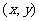 满足不等式
满足不等式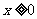 ,所以这条抛物线在
,所以这条抛物线在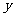 轴的右侧;当
轴的右侧;当 的值增大时,|
的值增大时,|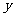 |也增大,这说明抛物线向右上方和右下方无限延伸。
|也增大,这说明抛物线向右上方和右下方无限延伸。
例1 (1)(口答)已知抛物线标准方程是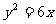 ,则它的焦点坐标为
,则它的焦点坐标为 ,
,
准线 的方程为
的方程为
解:(1)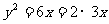
p=3,焦点坐标是(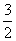 ,0)准线方程是x=-
,0)准线方程是x=-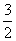 .
.
即学即练1
(2)(口答)已知抛物线的焦点坐标是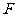 (2,0),则它的标准方程是
(2,0),则它的标准方程是 。
。
解:焦点在 轴的正半轴上,设抛物线标准方程是
轴的正半轴上,设抛物线标准方程是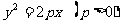
因为焦点坐标是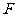 (2,0)
(2,0)
所以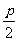 =2,
=2,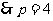
所求抛物线的标准方程是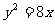 .
.
即学即练2
(3)(口答)已知抛物线的准线方程是x=-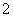 ,则它的标准方程是
,则它的标准方程是 。
。
解:因为抛物线的准线方程是x=-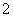 ,所以焦点在
,所以焦点在 轴的正半轴上,
轴的正半轴上,
设抛物线标准方程是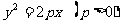
所以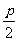 =2,
=2,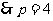
所求抛物线的标准方程是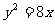 .
.
即学即练3
(4) 点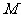 与点
与点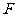 (4,0)的距离和它到直线
(4,0)的距离和它到直线 的距离相等,求点
的距离相等,求点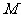 的轨迹方程
的轨迹方程
(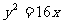 )
)
(5)点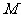 与点
与点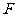 (4,0)的距离比它到直线
(4,0)的距离比它到直线 的距离小1,求点
的距离小1,求点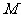 的轨迹方程
的轨迹方程
解法一:可知原条件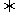 M点到F(4,0)和到x=-4距离相等,由抛物线的定义,点M的轨迹是以F(4,0)为焦点,x=-4为准线的抛物线.
M点到F(4,0)和到x=-4距离相等,由抛物线的定义,点M的轨迹是以F(4,0)为焦点,x=-4为准线的抛物线.
∴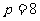
 所求方程是
所求方程是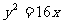

解法二:用直接法求点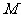 的轨迹方程
的轨迹方程
(四)数形结合思考:
在方程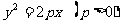 中,因为一次项系数为_____,可以得到焦点坐标_________,可以说:一次项系数是
中,因为一次项系数为_____,可以得到焦点坐标_________,可以说:一次项系数是 ,则交点在
,则交点在 轴上,且焦点的横坐标等于一次项
轴上,且焦点的横坐标等于一次项 的系数的四分之一,同时也可以得到准线方程___________。反之,如果已知焦点的坐标是
的系数的四分之一,同时也可以得到准线方程___________。反之,如果已知焦点的坐标是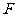 (
(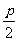 ,0),可以写出,抛物线方程____________;同理,如果已知准线方程是
,0),可以写出,抛物线方程____________;同理,如果已知准线方程是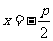 ,也可以写出,抛物线方程____________。
,也可以写出,抛物线方程____________。
(三) 探究二:抛物线的标准方程
问题1:坐标系应如何建立:
(1) 以定直线为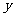 轴,过
轴,过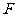 做定直线的垂线为
做定直线的垂线为 轴;
轴;
(2) 过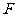 做定直线的垂线为
做定直线的垂线为 轴,以抛物线与
轴,以抛物线与 轴交点为原点,再画出
轴交点为原点,再画出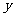 轴
轴
分析上两方案哪一个更好些?
问题2:抛物线的标准方程的推导:
如图所示,取经过点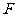 且垂直
且垂直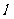 的直线为
的直线为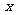 轴,垂足为
轴,垂足为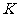 。以
。以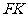 的中点
的中点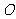 为原点,建立直角坐标系系,设|
为原点,建立直角坐标系系,设|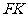 |=
|=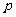 (
(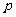 >0),
>0),
那么焦点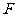 的坐标为
的坐标为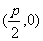 ,准线
,准线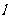 的方程为
的方程为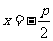 ,
,
设抛物线上的点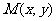 ,动点
,动点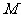 满足的几何条件是
满足的几何条件是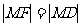
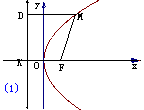 则有
则有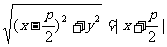

化简方程得 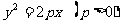

方程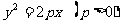 叫做抛物线的标准方程
叫做抛物线的标准方程
它表示的抛物线的焦点在 轴的正半轴上,焦点坐标是
轴的正半轴上,焦点坐标是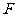 (
(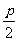 ,0),它的准线方程是
,0),它的准线方程是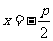 。
。
(二) 抛物线的定义
1、定义:平面内与一个定点F和一条不经过定点F的定直线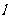 的距离_____(相等)的点的轨迹叫做_______(抛物线)
的距离_____(相等)的点的轨迹叫做_______(抛物线)
定点F叫做抛物线的焦点,定直线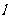 叫做抛物线的准线
叫做抛物线的准线
2、定义深化:
(1)定直线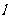 不经过定点F
不经过定点F
(2)定点F到定直线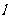 的距离记为
的距离记为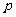 (
(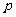 >0)
>0)
3、注意两个距离相等,可互相转换
(一)探究一:抛物线的定义
 问题:当
问题:当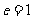 时,在平面内与一定点的距离和一条定直线的距离的比是常数
时,在平面内与一定点的距离和一条定直线的距离的比是常数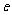 =1的点的轨迹是什么?
=1的点的轨迹是什么?
同学们自己动手画 l
(1)平面内一个定点F和一条不经过定点F的定直线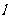
(2)在直线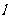 上任取点H,过点H作
·F
上任取点H,过点H作
·F
(3)作线段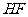 的垂直平分线
的垂直平分线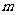 ,交
,交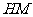 于
于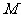
探究思考:当点H在直线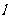 上运动时,
上运动时,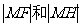 的大小关系?
的大小关系?
当点H在直线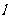 上运动时,总有___________(
上运动时,总有___________(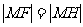 ),即动点M到定点F的距离和到定直线
),即动点M到定点F的距离和到定直线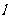 的距离____(相等)
的距离____(相等)
(5)动点M的轨迹是__________(一条抛物线)
椭圆和双曲线的有共同的几何特征:都可以看作是,在平面内与一定点的距离和一条定直线的距离的比是常数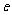 的点的轨迹。(其中定点不在直线上)
的点的轨迹。(其中定点不在直线上)
当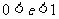 时,轨迹是椭圆;当
时,轨迹是椭圆;当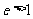 时,轨迹是双曲线。
时,轨迹是双曲线。
(1)范围
(2)对称性
(3)顶点
(4)离心率
(5)通径
(6)光学性质
(1)已知点A 与抛物线
与抛物线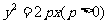 的焦点的距离是
的焦点的距离是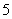 , 则
, 则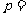
(2)抛物线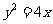 的弦AB垂直
的弦AB垂直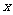 轴,若|AB|=
轴,若|AB|= , 则焦点到AB的距离为
, 则焦点到AB的距离为
(3)已知直线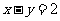 与抛物线
与抛物线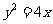 交于A、B两点,那么线段AB的中点坐标是 __
交于A、B两点,那么线段AB的中点坐标是 __
例1.已知抛物线关于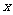 轴对称,它的顶点在坐标原点,并且经过点
轴对称,它的顶点在坐标原点,并且经过点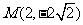 ,求它的标准方
,求它的标准方
程,并用描点法画出图形.
解法一:
解法二:
例2.探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处.已知灯口圆的直径为
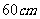 ,灯深
,灯深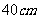 ,求抛物线的标准方程和焦点位置.
,求抛物线的标准方程和焦点位置.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com