
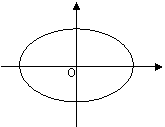
联立 
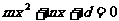
 韦达
韦达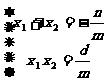 交点为
交点为
求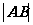 的一般办法:设已知直线为
的一般办法:设已知直线为  ,与已知曲线C的交点为
,与已知曲线C的交点为 ,
,
则有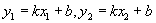 ,即
,即 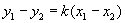
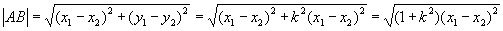
例2:已知椭圆C :x2 +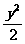 =1与直线l :
=1与直线l :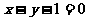 相交于A、B两点,求AB中点M坐标(中点坐标公式:
相交于A、B两点,求AB中点M坐标(中点坐标公式: )
)
变式2:已知斜率为1的直线l过椭圆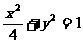 的右焦点,交椭圆于A、B两点,求弦AB的长。
的右焦点,交椭圆于A、B两点,求弦AB的长。
联立 



例1.当m为何值时,直线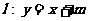 与椭圆
与椭圆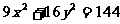 相切,相交,相离?
相切,相交,相离?
 变式1:已知椭圆
变式1:已知椭圆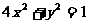 及直线
及直线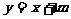 (1)当直线和椭圆有公共点时,求实数m的取值范围。(2)求被椭圆截得的最长弦所在的直线方程。
(1)当直线和椭圆有公共点时,求实数m的取值范围。(2)求被椭圆截得的最长弦所在的直线方程。
4. 你对老师的教学有哪些想法,请告诉老师.
3. 你还有哪些地方不清楚的,请告诉老师.
2.你在哪些数学能力上有所提高?
1.你认为有哪些主要的知识点? 你认为这节课的重点是什么?
例2(1)抛物线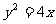 上一点
上一点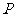
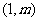 到焦点F的距离是
到焦点F的距离是
解: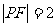
(2) 抛物线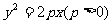 上一点
上一点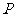
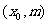 到焦点F的距离是
到焦点F的距离是
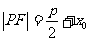
规纳总结:
定义:抛物线上任意一点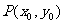 与抛物线焦点
与抛物线焦点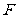 的连线段,叫做抛物线的焦半径
的连线段,叫做抛物线的焦半径
抛物线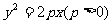 焦半径公式是:
焦半径公式是:
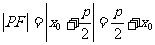
(3)斜率为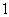 的直线经过抛物线
的直线经过抛物线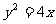 的焦点,与抛物线相交于两点
的焦点,与抛物线相交于两点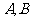 ,
,
求线段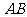 的长。
的长。
分析:利用根与系数关系及抛物线的定义来解之。
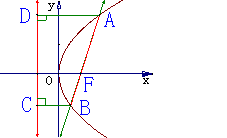 解:如图,由抛物线的标准方程可知,抛物线焦点的坐标为
解:如图,由抛物线的标准方程可知,抛物线焦点的坐标为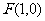 ,设
,设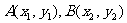 所以直线
所以直线 的方程为
的方程为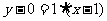
即 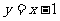 ①
①
将方程①代入抛物线方程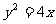 ,得
,得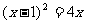
化简得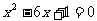
由抛物线的定义可知,|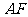 |等于点
|等于点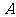 到准线
到准线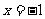 的距离|
的距离|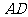 |,而|
|,而|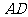 |=
|=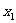 +1.同理|
+1.同理|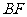 |=|
|=|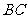 |=
|=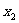 +1,于是得
+1,于是得
|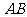 |=|
|=|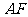 |+|
|+|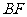 |=
|=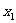 +
+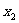 +2。
+2。
根据根与系数的关系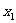 +
+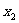 =6。
=6。
|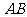 |=6+2=8。
|=6+2=8。
规纳总结:抛物线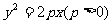 的焦点弦长公式|
的焦点弦长公式|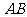 |=
|=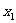 +
+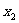 +
+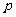
小结归纳:
引申探究:(4)求经过抛物线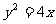 的焦点的弦
的焦点的弦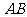 的中点的轨迹方程
的中点的轨迹方程
解:(点差法)设 ,
,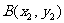 ,
,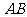 中点
中点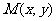 ,因为
,因为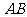 在抛物线
在抛物线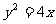 上,所以有
上,所以有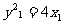 ①,
①,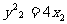 ②,① -②得,化简整理得
②,① -②得,化简整理得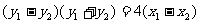
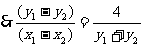 ,
,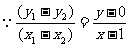 ,
,
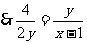 ,
, 为所求的直线
为所求的直线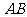 的方程。
的方程。
4、离心率
抛物线上的点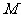 与焦点
与焦点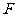 的距离和它到准线的距离的比,叫做抛物线的离心率,用
的距离和它到准线的距离的比,叫做抛物线的离心率,用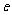 表示.
表示.
由抛物线的定义可知,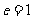 。
。
3、顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程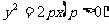 中,当
中,当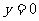 时,
时,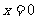 ,因此抛物线
,因此抛物线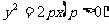 的顶点就是坐标原点.
的顶点就是坐标原点.
2、对称性
以-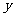 代
代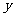 ,方程
,方程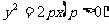 不变,所以这条抛物线关于
不变,所以这条抛物线关于 轴对称,我们把抛物线的对称轴叫做抛物线的轴。
轴对称,我们把抛物线的对称轴叫做抛物线的轴。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com