
2、(2008江苏苏州)小明利用一未知焦距的凸透镜探究透镜的成像规律,进
 行了如下操作并得到了相关结论.请你将空缺部分补充
行了如下操作并得到了相关结论.请你将空缺部分补充
完整。
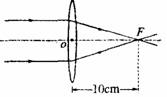
(1)将一束平行光射向凸透镜,得到如图所示的光路图.
则该透镜的焦距为 cm.
(2)将蜡烛、透镜和光屏放在光具座上,并使烛焰、透镜和光屏三者的中心大致在 .
 (3)按要求进行观察和测量,并将观测情况记录在下表中.
(3)按要求进行观察和测量,并将观测情况记录在下表中.
①上表中实验序号2中像的性质为 ,实验序号4中像距为 cm
②当烛焰从远处向透镜靠近时,仍要在光屏上得到清晰的像,光屏应向 (选填
“靠近”或“远离”)透镜的方向移动.
1、(2008山东烟台)在探究凸透镜成像的实验中:
(1)在探究前,小明同学将凸透镜对着太阳光,把透镜逐渐向白纸移动,直到太阳光在白纸上会聚到一点(图甲).这一操作的目的是__________________________________________。
(2)小明将蜡烛、凸透镜和光屏放入光具座中进行实验.其中一次实验情景如图乙所示;由此得到的实验结论___________________________________________________________。
4、(2008山东青岛)进一步探究:
小宇从《物理手册》中查到光从玻璃射向空气中的一些数据:
|
入射角i |
0° |
30° |
39° |
39°30' |
40° |
50° |
|
折射角r |
0° |
51° |
79° |
82° |
90° |
|
|
反射的能量 |
4.7% |
6.8% |
36% |
47% |
100% |
100% |
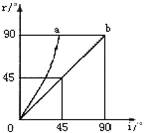 ①当入射角i≥ 时,不发生折射现象。图像中的图线 反映了上述实验中的两角关系。
①当入射角i≥ 时,不发生折射现象。图像中的图线 反映了上述实验中的两角关系。
②判断:如果光从空气射向玻璃,则反射的能量可以达到100%。( )
 凸透镜成像规律
凸透镜成像规律
3.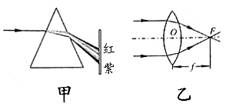 (2007年河南省)如图所示,冬冬在探究光的色散现象时,看到白光经三棱镜后,光屏上自上而下出现了红、橙、黄、绿、蓝、靛、紫的色带,冬冬对产生的原因进行了思考。受此启发,在测量凸透镜的焦距时,冬冬想:如果分别用红光和紫光平行于同一个凸透镜的主光轴射入,红光、紫光对凸透镜的焦距是否不同呢?请写出你的推断: 色光对凸透镜的焦距大,你推断的理由是:
。
(2007年河南省)如图所示,冬冬在探究光的色散现象时,看到白光经三棱镜后,光屏上自上而下出现了红、橙、黄、绿、蓝、靛、紫的色带,冬冬对产生的原因进行了思考。受此启发,在测量凸透镜的焦距时,冬冬想:如果分别用红光和紫光平行于同一个凸透镜的主光轴射入,红光、紫光对凸透镜的焦距是否不同呢?请写出你的推断: 色光对凸透镜的焦距大,你推断的理由是:
。
1、(云南省2008)(5分)小宇利用图所示装置将一细光束斜射到空气中,用于探究“光的折射规律”。
 (1)为了更清晰地观察水中的光路。可以采用的办法是:
(1)为了更清晰地观察水中的光路。可以采用的办法是:
。
实验中, (填“能”或“不能”)看见反射光线。
(2)实验的折射光路如图中所示,可以判定折射角
填 “大于”、“小于”或“等于”)入射角。增大入射角观察到
折射角在 (填“增大”或“减小”)。 若不断增
大光在水中的入射角,会观察到的现象是:入射角到一定值时,
。
40、若定义在区间 上的函数
上的函数 对
对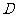 上的任意
上的任意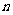 个值
个值 ,
, ,…,
,…,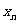 ,总满足
,总满足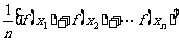 ≤
≤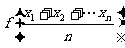 ,则称
,则称 为
为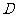 上的凸函数.已知函数
上的凸函数.已知函数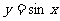 在区间
在区间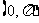 上是“凸函数”,则在△
上是“凸函数”,则在△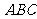 中,
中,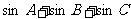 的最大值是____________________.
的最大值是____________________.
答案:1 C 、 2 C 、3 A 、4 B 、5 D 、6 B 、7 D 、8 A 、9 C 、10 C 、11 B 、12 C 、13 C、14 C 、15 B 、 16 B 、17 A 、18 D 、19 A 、20 B 、
21 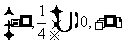 、 22
、 22 、 23
、 23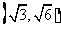 、 24 10、 25 2、 26
、 24 10、 25 2、 26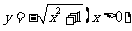 27
27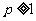 、 28
、 28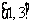 、 29
、 29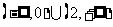 、 30
、 30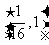 、 31
、 31  32
32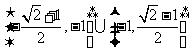 、 33 2、 34
、 33 2、 34  、35
、35 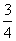 或
或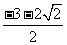 、 36
4、
37
、 36
4、
37 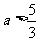 或
或 、 38
、 38 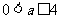 或
或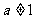 、 39
、 39 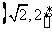 、40
、40 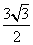 。
。
39、若曲线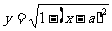 与
与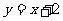 有且只有一个公共点
有且只有一个公共点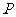 ,
,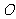 为坐标原点,则
为坐标原点,则
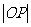 的取值范围是________________________.
的取值范围是________________________.
38、若函数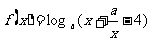 (
( >0且
>0且 ≠1)的值域为
≠1)的值域为 ,则实数
,则实数 的取值范围是________________.
的取值范围是________________.
37、已知函数 的定义域为
的定义域为 ,则实数
,则实数 的取值范围是________________________.
的取值范围是________________________.
36、对于任意实数 、
、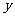 ,定义运算
,定义运算 *
*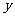 为:
为: *
*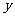 =
=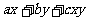 ,其中
,其中 、
、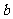 、
、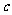 为常数,等式右边的运算是通常的加法和乘法运算,现已知1*2=3,2*3=4,并且有一个非零常数
为常数,等式右边的运算是通常的加法和乘法运算,现已知1*2=3,2*3=4,并且有一个非零常数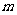 ,使得对于任意实数
,使得对于任意实数 ,都有
,都有 *
*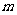 =
= ,则
,则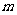 =______________________.
=______________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com