
4.不等式的解法
(1)作用与地位
解不等式是求定义域、值域、参数的取值范围时的重要手段,与“等式变形”并列的“不等式的变形”,是研究数学的基本手段之一。
高考试题中,对解不等式有较高的要求,近两年不等式知识占相当大的比例。
(2)一元一次不等式(组)及一元二次不等式(组)
解一元一次不等式(组)及一元二次不等式(组)是解其他各类不等式的基础,必须熟练掌握,灵活应用。
(3)高次不等式
解高次不等式常用“数轴标根法”。一般地,设多项式
F(x)=a(x-a1)(x-a2)…(x-an) (a≠0)
它的n个实根的大小顺序为a1<a2<…<an,把数轴分成n+1个区间:
(-∞,a1),(a1,a2),…,(an-1,an),(an,+∞)
自右至左给这些区间编上顺序号,则当a>0时有:
①在奇数区间内,F(x)>0。
②在偶数区间内,F(x)<0
(4)分式不等式
分式不等式的等价变形:
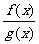 >0
>0 f(x)·g(x)>0
f(x)·g(x)>0
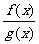 ≥0
≥0
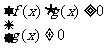
(5)无理不等式
两类常见的无理不等式等价变形:
 ≥g(x)
≥g(x) 
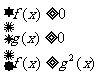 或
或
 <g(x)
<g(x) 

(6)指数不等式与对数不等式
①当0<a<1时
a(fx)>ag(x) f(x)<g(x)
f(x)<g(x)
②当a>1时
a(fx)>ag(x) f(x)>g(x)
f(x)>g(x)
logaf(x)>logag(x) f(x)>g(x)>0
f(x)>g(x)>0
(7)含参数不等式
对于解含参数不等式,要充分利用不等式的性质。对参数的讨论,要不“重复”不“遗漏”。
3.不等式的证明
(1)作用地位
证明不等式是数学的重要课题,也是分析、解决其他数学问题的基础,特别是在微积分中,不等式是建立极限论的理论基础。
高考中,主要涉及“a,b>0时,a+b≥2 ”这类不等式,以及运用不等式性质所能完成的简单的不等式的证明。用数学归纳法证明的与自然数有关命题的不等式难度较大。
”这类不等式,以及运用不等式性质所能完成的简单的不等式的证明。用数学归纳法证明的与自然数有关命题的不等式难度较大。
(2)基本不等式
定理1:如果a,b∈{x|x是正实数},那么 ≥
≥ (当且仅当a=b时取“=”号)
(当且仅当a=b时取“=”号)
定理2:如果a,b,c∈{x|x是正实数},那么 ≥
≥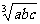 (当且仅当a=b=c时取“=”号)
(当且仅当a=b=c时取“=”号)
定理3:如果a、b∈{x|x是正实数},那么
 ≤
≤ ≤
≤ ≤
≤
(当且仅当a=b时取“=”号)
推论4:如果a,b,c∈{x|x是正实数},那么
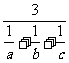 ≤
≤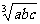 ≤
≤ ≤
≤
(当且仅当a=b=c时取“=”号)
由上述公式还可衍生出一些公式
①4ab≤(a+b)2≤2(a2+b2),a、b∈R(当且仅当a=b时等号成立)
②a2+b2+c2≥ab+bc+ca,a,b,c∈R(当且仅当a=b=c时等号成立)
③a2+b2+c2≥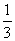 (a+b+c)2≥ab+bc+ca,a,b,c∈R(当且仅当a=b=c时等号成立)
(a+b+c)2≥ab+bc+ca,a,b,c∈R(当且仅当a=b=c时等号成立)
④|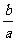 +
+ |≥2(当且仅当|a|=|b|时取“=”号)
|≥2(当且仅当|a|=|b|时取“=”号)
⑤a>0,b>0,a+b=1,则ab≤ 等。
等。
(4)不等式证明的三种基本方法
①比较法:作差比较,根据a-b>0 a>b,欲证a>b只需证a-b>0;作商比较,当b>0时,a>b
a>b,欲证a>b只需证a-b>0;作商比较,当b>0时,a>b
 >1。比较法是证明不等式的基本方法,也是最重要的方法,有时根据题设可转化为等价问题的比较(如幂、方根等)。
>1。比较法是证明不等式的基本方法,也是最重要的方法,有时根据题设可转化为等价问题的比较(如幂、方根等)。
②分析法:从求证的不等式出发寻找使该不等式成立的充分条件。对于思路不明显,感到无从下手的问题宜用分析法探究证明途径。
③综合法:从已知的不等式及题设条件出发,运用不等式性质及适当变形(恒等变形或不等变形)推导出要求证明的不等式。
2.不等式的性质
(1)作用地位
不等式性质是不等式理论的基本内容,在证明不等式、解不等式中都有广泛的应用。高考中,有时直接考查不等式的性质,有时间接考查性质(如在证明不等式、解不等式中就间接考查了掌握不等式性质的程度)。准确地认识、运用基本性质,并能举出适当反例,能辨别真假命题是学好不等式的要点。
(2)基本性质
实数大小比较的原理与实数乘法的符号法则是不等式性质的依据。在不等式性质中,最基本的是:
①a>b b<a(对称性)
b<a(对称性)
②a>b,b>c a>c(传递性)
a>c(传递性)
③a>b a+c>b+c(数加)
a+c>b+c(数加)
④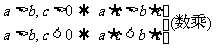
(a>b,c=0 a·c=b·c)
a·c=b·c)
与等式相比,主要区别在数乘这一性质上,对于等式a=b ac=bc,不论c是正数、负数还是零,都成立,而对于不等式a>b,两边同乘以c之后,ac与bc的大小关系就需对c加以讨论确定。这关系即使记得很清楚,但在解题时最容易犯的毛病就是错用这一性质,尤其是需讨论参数时。
ac=bc,不论c是正数、负数还是零,都成立,而对于不等式a>b,两边同乘以c之后,ac与bc的大小关系就需对c加以讨论确定。这关系即使记得很清楚,但在解题时最容易犯的毛病就是错用这一性质,尤其是需讨论参数时。
(3)基本性质的推论
由基本性质可得出如下推论:
推论1:a>b>0,c>d>0 ac>bd
ac>bd
推论2:a>b>0,c>d>0

推论3:a>b>0 an>bn(n∈N)
an>bn(n∈N)
推论4:a>b>0
 (n∈N)
(n∈N)
对于上述推论可记住两点:一是以上推论中a,b,c,d均为正数,即在{x|x是正实数}中对不等式实施运算;二是直接由实数比较大小的原理出发。
1.不等式知识相互关系表

3.会用不等式||a|-|b||≤|a+b|≤|a|+|b|。
2.在熟练掌握一元一次不等式(组)、一元二次不等式(组)的解法的基础上初步掌握其他的一些简单的不等式的解法。
1.掌握不等式的性质及其证明,掌握证明不等式的几种常用方法,掌握两个和三个(不要求四个和四个以上)“正数的算术平均数不小于它们的几何平均数”这两个定理,并能运用上述性质、定理和方法解决一些问题。
不等式,不等式的性质,不等式的证明,不等式的解法,含有绝对值的不等式。
22.设f(x)=ax2+bx+c,若f(1)=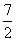 ,问是否存在a、b、c∈R,使得不等式:
,问是否存在a、b、c∈R,使得不等式:
x2+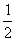 ≤f(x)≤2x2+2x+
≤f(x)≤2x2+2x+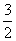 对一切实数x都成立,证明你的结论。
对一切实数x都成立,证明你的结论。
21.已知函数f(x)=x2+px+q,对于任意θ∈R,有f(sinθ)≤0,且f(sinθ+2)≥0;
(1)求p、q之间的关系式;
(2)求p的取值范围;
(3)如果f(sinθ +2)的最大值是14,求p的值,并求此时f(sinθ)的最小值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com