
7.(本小题满分14分)
设函数 在
在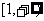 上是增函数.
上是增函数.
(1)
求正实数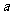 的取值范围;
的取值范围;
(2)
设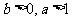 ,求证:
,求证:
解:(1) 对
对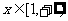 恒成立,
恒成立,
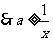 对
对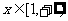 恒成立
恒成立
又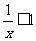
 为所求.…………………………4分
为所求.…………………………4分
(2)取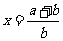 ,
,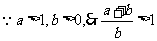 ,
,
一方面,由(1)知 在
在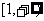 上是增函数,
上是增函数,


即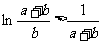 ……………………………………8分
……………………………………8分
另一方面,设函数
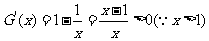
∴ 在
在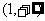 上是增函数且在
上是增函数且在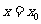 处连续,又
处连续,又
∴当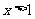 时,
时,
∴ 即
即
综上所述, ………………………………………………14分
………………………………………………14分
又MN⊥MQ,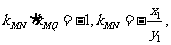 所以
所以
直线QN的方程为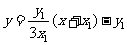 ,又直线PT的方程为
,又直线PT的方程为 ……10分
……10分
从而得 所以
所以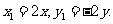
代入(1)可得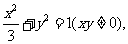 此即为所求的轨迹方程.………………13分
此即为所求的轨迹方程.………………13分
6.(本小题满分12分)
过抛物线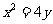 上不同两点A、B分别作抛物线的切线相交于P点,
上不同两点A、B分别作抛物线的切线相交于P点,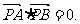
(1)求点P的轨迹方程;
(2)已知点F(0,1),是否存在实数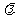 使得
使得 ?若存在,求出
?若存在,求出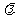 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
解法(一):(1)设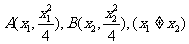
由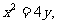 得:
得: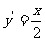
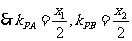
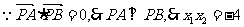 ………………………………3分
………………………………3分
直线PA的方程是: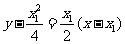 即
即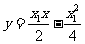 ①
①
同理,直线PB的方程是: ②
②
由①②得:
∴点P的轨迹方程是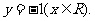 ……………………………………6分
……………………………………6分
(2)由(1)得: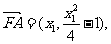
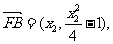
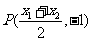
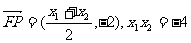
 …………………………10分
…………………………10分

所以
故存在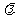 =1使得
=1使得 …………………………………………12分
…………………………………………12分
解法(二):(1)∵直线PA、PB与抛物线相切,且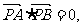
∴直线PA、PB的斜率均存在且不为0,且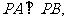
设PA的直线方程是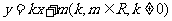
由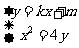 得:
得: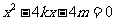
 即
即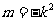 …………………………3分
…………………………3分
即直线PA的方程是: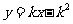
同理可得直线PB的方程是: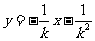
由 得:
得: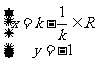
故点P的轨迹方程是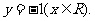 ……………………………………6分
……………………………………6分
(2)由(1)得:

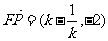
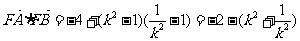 ………………………………10分
………………………………10分
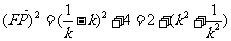
故存在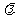 =1使得
=1使得 …………………………………………12分
…………………………………………12分
3.解析:(1)设行李包在空中运动时间为t,飞出的水平距离为s,则 ①
①
s=vt ②
代入数据得:t=0.3s ③
s=0.9m ④
(2)设行李包的质量为m,与传送带相对运动时的加速度为a,则
滑动摩擦力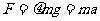 ⑤
⑤
代入数据得:a=2.0m/s2 ⑥
要使行李包从B端飞出的水平距离等于(1)中所求水平距离,行李包从B端飞出的水平抛出的初速度v=3.0m/s
设行李被加速到时通过的距离为s0,则  ⑦
⑦
代入数据得s0=2.0m ⑧
故传送带的长度L应满足的条件为:L≥2.0m
1、解析:设抛出点的高度为h,第一次平抛的水平射程为x,则有x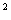 +y
+y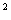 =L
=L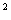
由平抛运动的规律得知,当初速度增大到2倍,其水平射程也增大到2x,可得(2x)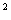 +h
+h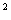 =(
=( L)
L)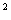
由以上两式解得h=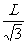
设该星球上的重力加速度为g,由平抛运动的规律得h= gt
gt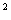
由万有引力定律与牛顿第二定律得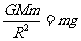 (式中m为小球的质量)
(式中m为小球的质量)
联立以上各式得: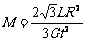 。
。
评注:显然,在本题的求解过程中,必须将自己置身于该星球上,其实最简单的办法是把地球当作该星球是很容易身临其境的了。
解:(1) 电流为零时金属杆所处的位置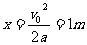
(2) 电流的最大值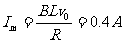
金属直杆在向右运动的过程中, ,得F=-0.18N,"-"说明F指向x轴负方向。
,得F=-0.18N,"-"说明F指向x轴负方向。
金属直杆在向右运动的过程中,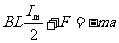 ,得F=-0.22N,"-"说明F指向x轴负方向。
,得F=-0.22N,"-"说明F指向x轴负方向。
(3)由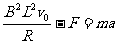 ,得
,得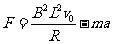
所以,当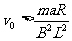 时,
时,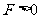 。F指向x轴正方向。
。F指向x轴正方向。
当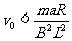 时,
时, 。F指向x轴负方向。
。F指向x轴负方向。
3.(20分)如图所示为车站使用的水平传送带装置的示意图.绷紧的传送带始终保持3.0m/s的恒定速率运行,传送带的水平部分AB距水平地面的高度为A=0.45m.现有一行李包(可视为质点)由A端被传送到B端,且传送到月端时没有被及时取下,行李包从B端水平抛出,不计空气阻力,g取l0m/s2
(1)若行李包从B端水平抛出的初速v=3.0m/s,求它在空中运动的时间和飞出的水平距离;
 (2)若行李包以v0=1.0m/s的初速从A端向右滑行,包与传送带间的动摩擦因数μ=0.20,要使它从B端飞出的水平距离等于(1)中所求的水平距离,求传送带的长度L应满足的条件.
(2)若行李包以v0=1.0m/s的初速从A端向右滑行,包与传送带间的动摩擦因数μ=0.20,要使它从B端飞出的水平距离等于(1)中所求的水平距离,求传送带的长度L应满足的条件.
2010届计算题拿分训练(4)答案
2. (18分)如图所示,两条互相平行的光滑金属导轨位于水平面内,距离为L= 0.2m,在导轨的一端接有阻值为R=0.5Ω的电阻,在x≥0处有一与水平面垂直的均匀磁场,磁感强度B= 0.5T。一质量为m = 0. lkg的金属直杆垂直放置在导轨上,并以v0 = 2m/s的初速度进入磁场,在安培力和一垂直于杆的水平外力F的共同作用下作匀变速直线运动,加速度大小为a=2m/s2、方向与初速度方向相反。设导轨和金属杆的电阻都可以忽略,且接触良好。求:
(18分)如图所示,两条互相平行的光滑金属导轨位于水平面内,距离为L= 0.2m,在导轨的一端接有阻值为R=0.5Ω的电阻,在x≥0处有一与水平面垂直的均匀磁场,磁感强度B= 0.5T。一质量为m = 0. lkg的金属直杆垂直放置在导轨上,并以v0 = 2m/s的初速度进入磁场,在安培力和一垂直于杆的水平外力F的共同作用下作匀变速直线运动,加速度大小为a=2m/s2、方向与初速度方向相反。设导轨和金属杆的电阻都可以忽略,且接触良好。求:
(1)电流为零时金属杆所处的位置
(2)电流为最大值的一半时施加在金属杆上外力F的大小和方向
(3)保持其他条件不变,而初速度v0取不同值,求开始时F的方向与初速度v0取值的关系
1.(17分)宇航员站在某一星球表面上的某高处,沿水平方向抛出一小球。经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L。若抛出时的初速度增大到2倍,则抛出点与落地点之间的距离为 L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
2.证明不等式的常用方法
除了课本上介绍的证明不等式的三种基本方法外,还有如下常用方法:
(1)放缩法
若证明“A≥B”,我们先证明“A≥C”,然后再证明“C≥B”,则“A≥B”。
(2)反证法
反证法是通过否定结论导致矛盾,从而肯定原结论的一种方法。
(3)数学归纳法
证明与自然数n有关的不等式时,常用数学归纳法。此法高考中已多次考查。
(4)变量代换法
变量代换是数学中的一种常用的解题方法,对于一些结构比较复杂,变化较多而关系不太清楚的不等式,可适当地引进一些新的变量进行代换,以简化其结构。其代换技巧有局部代换、整体代换、三角代换、增量代换等。
(5)函数方法
通过利用函数的性质,如单调性、凹凸性、有界性、实根存在的条件等证明不等式的方法称为函数方法。
(6)构造方法
不等式证明中的构造方法,主要是指通过引进合适的恒等式、数列、函数、图形及变量等辅助手段,促使命题转化,从而使不等式得证。此法技巧要求较高,高考试题中很少见。
[例题解析]
例1 证明下列不等式:
(1)若x,y,z∈R,a,b,c∈{x|x是正实数},则
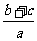 x2+
x2+ y2+
y2+ z2≥2(xy+yz+zx);
z2≥2(xy+yz+zx);
(2)若x,y,z∈{x|x是正实数},且x+y+z=xyz,则 +
+ +
+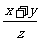 ≥2(
≥2(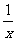 +
+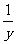 +
+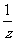 )2。
)2。
解 (1)先考虑用作差证法
∵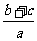 x2+
x2+ y2+
y2+ z2-2(xy+yz+zx)= (
z2-2(xy+yz+zx)= (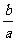 x2+
x2+ y2-2xy)+(
y2-2xy)+(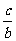 y2+
y2+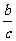 z2-2yz)+
z2-2yz)+
(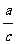 z2+
z2+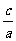 x2-2zx)=(
x2-2zx)=(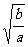 x
x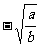 y)2+(
y)2+( y-
y-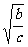 z)2+(
z)2+(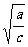 z-
z-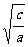 x)2≥0
x)2≥0
∴ 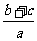 x2+
x2+ y2+
y2+ z2≥2(xy+yz+zx)
z2≥2(xy+yz+zx)
(2)采用等价转化法
所证不等式等价于
x2y2z2( +
+ +
+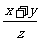 )≥2(xy+yz+zx)2
)≥2(xy+yz+zx)2
 xyz·[yz(y+z)+zx(z+x)+xy(x+y)]≥2(xy+yz+zx)2
xyz·[yz(y+z)+zx(z+x)+xy(x+y)]≥2(xy+yz+zx)2
 (x+y+z)(y2z+yz2+z2x+zx2+x2y+xy2)≥2(x2y2+y2z2+z2x2)+4(x2yz+xy2z+xyz2)
(x+y+z)(y2z+yz2+z2x+zx2+x2y+xy2)≥2(x2y2+y2z2+z2x2)+4(x2yz+xy2z+xyz2)
 y3z+yz3+z3x+zx3+x3y+xy3≥2x2yz+2xy2z+2xyz2
y3z+yz3+z3x+zx3+x3y+xy3≥2x2yz+2xy2z+2xyz2
 yz(y-z) 2 +zx(z-x) 2+xy(x-y) 2+x2 (y-z)
2+y2 (z-x)2+z2 (x-y) 2≥0
yz(y-z) 2 +zx(z-x) 2+xy(x-y) 2+x2 (y-z)
2+y2 (z-x)2+z2 (x-y) 2≥0
∵上式显然成立 ∴原不等式得证。
注 (1)配方技巧的实现关键在于合理的分项,正是这种分项我们对(1)还可证明如下:
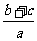 x2+
x2+ y2+
y2+ z2
z2
=(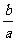 x2+
x2+ y2)+(
y2)+(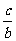 y2+
y2+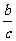 z2)+(
z2)+(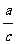 z2+
z2+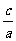 x2)
x2)
≥2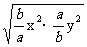 +2
+2 +2
+2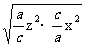
≥2(xy+yz+zx)
(2)的证法要害是:化分式为整式,活用条件,即用x+y+z代换xyz,以及配方技术。事实上,这个代数不等式的实质是如下三角不等式:
在锐角△ABC中,求证:
cotA(tanB+tanC)+cotB·(tanC+tanA)+cotC·(tanA+tanB)≥2(cotA+cotB+cotC)2
例2 证明若x,y,z∈R,且x+y+z=1,x2+y2+z2=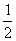 ,则x,y,z,∈[0,
,则x,y,z,∈[0, ]。
]。
证法一由x+y+z=1,x2+y2+z2=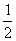 ,得:x2+y2+(1-x-y)2=
,得:x2+y2+(1-x-y)2=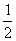
整理成关于y的一元二次方程得:
2y2-2(1-x)y+2x2-2x-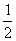 =0
=0
∵y∈R,故Δ≥0
4(1-x)2-4×2(2x2-2x-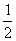 )≥0
)≥0
解之得:0≤x≤ ∴x∈[0,
∴x∈[0, ]
]
同理可得:y,z∈[0, ]
]
证法二
设x=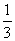 +x′,y=
+x′,y=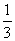 +y′,z=
+y′,z=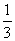 +z′,则x′+y′+z′=0
+z′,则x′+y′+z′=0
于是
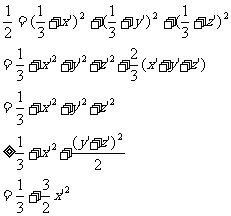
故 ,x′∈[-
,x′∈[-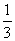 ,
,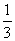 ],x∈[0,
],x∈[0,  ],同理,y,z∈[0,
],同理,y,z∈[0,  ]
]
证法三 反证法
设x、y、z三数中若有负数,不妨设x<0,则x2>0,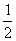 =x2+y2+z2≥x2+
=x2+y2+z2≥x2+ =
=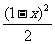 +x2=
+x2=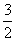 x2-x+
x2-x+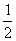 >
>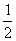 ,矛盾。
,矛盾。
设x,y,z三数中若有最大者大于 ,不妨设x>
,不妨设x> ,则:
,则:
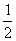 =x2+y2+z2≥x2+
=x2+y2+z2≥x2+
=x2+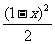 =
=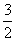 x2-x+
x2-x+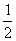
=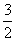 x·(x-
x·(x- )+
)+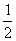 >
>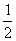 ,矛盾。
,矛盾。
故x,y,z∈[0,  ]。
]。
注:本题证法甚多,最易接受的方法是证法一的判别式法,因为该法思路明晰,易于操作,技巧性不强。
1.不等式中常见的基本思想方法
(1)等价转化。具体地说,就是无理化为有理,分式化为整式,高次化为低次,绝对值化为非绝对值,指数、对数化为代数式等。
(2)分类讨论。分类讨论的目的是处理解决问题过程中遇到的障碍,在无障碍时不要提前进行分类讨论。
(3)数形结合。有些不等式的解决可化为两个函数图像间的位置关系的讨论等几何问题。
(4)函数方程思想。解不等式可化为解方程或求函数图像与x轴交点的问题,根据题意判断所求解的区间。如“标根法”实际上就是一种函数方程思想。
5.含有绝对值的不等式
(1)作用与地位
绝对值不等式适用范围较广,向量、复数的模、距离、极限的定义等都涉及到绝对值不等式。
高考试题中,对绝对值不等式从多方面考查。
(2)两个基本定理
定理1:||a|-|b||≤|a+b|≤|a|+|b| (a、b∈R)
定理2:||a|-|b||≤|a-b|≤|a|+|b| (a、b∈R)
应理解其含义,掌握证明思路以及“=”号成立的条件。
(3)解绝对值不等式的常用方法
①讨论法:讨论绝对值中的式于大于零还是小于零,然后去掉绝对值符号,转化为一般不等式。
②等价变形:解绝对值不等式常用以下等价变形
|x|<a x2<a2
x2<a2 -a<x<a(a>0)
-a<x<a(a>0)
|x|>a x2>a2
x2>a2 x>a或x<-a(a>0)
x>a或x<-a(a>0)
一般地有:
|f(x)|<g(x) -g(x)<f(x)<g(x)
-g(x)<f(x)<g(x)
|f(x)|>g(x) f(x)>g (x)或f(x)<g(x)
f(x)>g (x)或f(x)<g(x)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com