
3.均匀分布在地球赤道平面上的三颗同步通信卫星能够实现除地球南北极等少数地区外的“全球通信”。已知地球半径为R,地球表面的重力加速度为g,同步卫星所在的轨道处的重力加速度为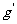 ,地球自转周期为T,下面列出的是关于三颗卫星中任意两颗卫星间距离s的表达式:
,地球自转周期为T,下面列出的是关于三颗卫星中任意两颗卫星间距离s的表达式:
A.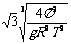 B.
B. C.
C. D.
D.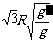
2. 如图甲、乙所示,是一辆质量为6×103kg的公共汽车在t=0和t=3s末两个时刻的两张照片.当t=0时,汽车刚启动,在这段时间内汽车的运动可看成匀加速直线运动.图丙是车内横杆上悬挂的拉手环经放大后的图像,q=37°,根据题中提供的信息,可以估算出的物理量有
如图甲、乙所示,是一辆质量为6×103kg的公共汽车在t=0和t=3s末两个时刻的两张照片.当t=0时,汽车刚启动,在这段时间内汽车的运动可看成匀加速直线运动.图丙是车内横杆上悬挂的拉手环经放大后的图像,q=37°,根据题中提供的信息,可以估算出的物理量有
A.汽车的长度 B.3s末汽车的速度
C.3s内合外力对汽车所做的功 D.3 s末汽车牵引力的功率
s末汽车牵引力的功率
1. 如图所示,在光滑水平面上,有两个相互接触的物体,若M>m,第一次用水平力F由左向右推M,两物体间的作用力为N1,第二次用同样大小的水平力F由右向左推m,两物体间的作用力为N2,则
如图所示,在光滑水平面上,有两个相互接触的物体,若M>m,第一次用水平力F由左向右推M,两物体间的作用力为N1,第二次用同样大小的水平力F由右向左推m,两物体间的作用力为N2,则
A.N1>N2 B.N1=N2
C.N1<N2 D.无法确定
21.(本小题满分13分)
设函数( )=
)=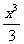 +
+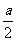
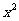 +b
+b +
+ (a,b,c
(a,b,c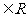 ),函数
),函数 (
( )的导数记为
)的导数记为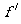 (
( )。
)。
(1)若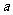
 =
=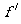 (2),b=
(2),b=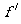 (1),c=
(1),c=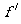 (0),求a,b,c的值;
(0),求a,b,c的值;
(2)若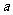 =
=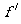 (2),b=
(2),b=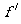 (1),c=
(1),c=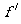 (0),且
(0),且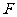 (
( )=
)=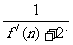 求证:
求证: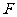 (1)+
(1)+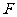 (2)+
(2)+
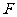 (3)+……+
(3)+……+ (
( )
)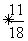 (
(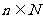 *);
*);
(3)设关于 的方程
的方程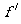 (
( )=0的两个实数根为
)=0的两个实数根为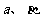 ,且1
,且1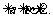 试问
试问 :是否存在正整数
:是否存在正整数 ,使得|
,使得|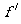 (
( )|
)|
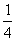 ?说明理由:
?说明理由:
解:(1)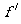 (
( )=
)=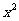 +
+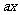 +
+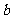 ,由已知可得
,由已知可得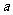 =-1,b=c=-3.……………………4分
=-1,b=c=-3.……………………4分
(2)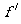 (
( )=
)=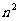 -
- -3,
-3,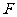 =(
=( )=
)=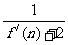 =
=
当 =1时,
=1时,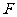 (1)=-1
(1)=-1 ;当
;当 =2时,
=2时,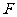 (1)+
(1)+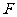 (2)=-1+
(2)=-1+ 1=0
1=0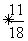 ;
;
当
 3时,
3时,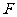 (
( )=
)=
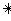
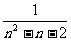 =
=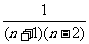 =
=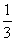 (
(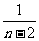 -
-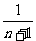 ).
).
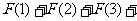 ……
……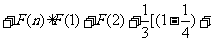

 ……
……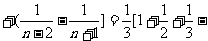
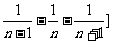
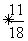 ,所以
,所以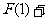
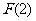
+ …+
…+ ………………………………………………9分
………………………………………………9分
(3)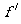
 .
.
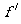 (1)
(1)

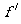 (2)=
(2)=
= ,
,
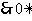 |
|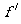 (1)1
(1)1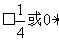 |
|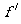 (2)|
(2)|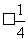 ,所以存在
,所以存在 =1或2,使|
=1或2,使|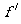 (
( )|
)| …13分
…13分
20.(本小题满分13分)
已知长方形ABCD, AB=6,BC=7/4.以AB的中点 为原点建立如图所示的平面直角坐标系
为原点建立如图所示的平面直角坐标系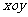
(1)求以A、B为焦点,且过C、D两点的椭圆C的标准方程;
 (2)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的点,
(2)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的点,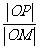 =λ,求点M的轨迹方程,并说明轨迹是什么曲线。
=λ,求点M的轨迹方程,并说明轨迹是什么曲线。
解:(1)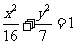 …………………5分
…………………5分
(2)设 ,其中
,其中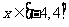 。由已知
。由已知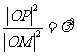 及点
及点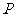 在椭圆
在椭圆 上可得
上可得
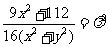 。整理得
。整理得 ,其中
,其中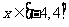 ……………8分
……………8分
(i)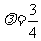 时。化简得
时。化简得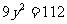
所以点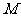 的轨迹方程为
的轨迹方程为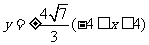 ,轨迹是两条平行于
,轨迹是两条平行于 轴的线段。
轴的线段。
(ii)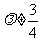 时,方程变形为
时,方程变形为 ,其中
,其中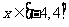
当 时,点
时,点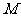 的轨迹为中
的轨迹为中 心在原点、实轴在
心在原点、实轴在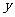 轴上的双曲线满足
轴上的双曲线满足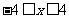 的部分。
的部分。
当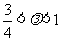 时,点
时,点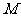 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在 轴上的椭圆满足
轴上的椭圆满足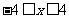 的部分;
的部分;
当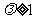 时,点
时,点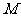 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在 轴上的椭圆………………13分
轴上的椭圆………………13分
19、(本小题满分13分)
有一座大桥既是交通拥挤地段,又是事故多发地段,为了保证安全,交通部门规定。大桥上的车距 与车速
与车速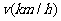 和车长
和车长 的关系满足:
的关系满足: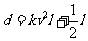 (
( 为正的常数),假定车身长为
为正的常数),假定车身长为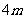 ,当车速为
,当车速为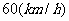 时,车距为2.66个车身长。
时,车距为2.66个车身长。
A. 写出车距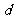 关于车速
关于车速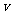 的函
的函 数关系式;
数关系式;
B. 应规定怎样的车速,才能使大桥上每小时通过的车辆最多?
解析:⑴因为当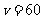 时,
时, ,所以
,所以 ……2分
……2分
∴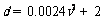 ………………………………………………………5分
………………………………………………………5分
⑵设每小时通过的车辆为 ,则
,则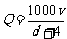 .即
.即
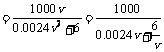 ……10分
……10分
∵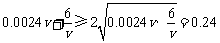 ,…………………………………………………12分
,…………………………………………………12分
∴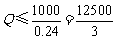 ,当且仅当
,当且仅当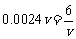 ,即
,即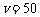 时,
时,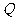 取最大值
取最大值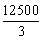 .
.
答:当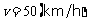 时,大桥每小时通过的车辆最多.………13分
时,大桥每小时通过的车辆最多.………13分
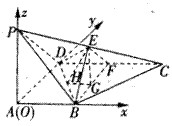
18.⑴如图,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴建立空间直角坐标系.
设AB=a,则易知点A、B、C、D、F的坐标分别为A(0,0,0), B(a,0,0),C(2a,2a,0),D(0,2a,0),F(a,2a,0). 从而
B(a,0,0),C(2a,2a,0),D(0,2a,0),F(a,2a,0). 从而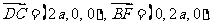

设 PA=b,则P(0,0,b),而E为PC的中点,故E(a,a,
PA=b,则P(0,0,b),而E为PC的中点,故E(a,a, ).
).
从而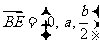 ,
,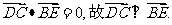
由此得CD⊥面BEF. ………………………………………………6分
⑵设E在xOy平面上的投影为G,作G作DH⊥BD,垂足为H.
由三垂线定理知EH⊥BD.
从而∠EHG为二面角E-BD-C的平面角.
由PA=k·AB得P(0,0,ka),E ,G
,G .
.
设H(x,y,0),则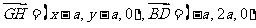 ,
,
由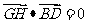 得-a(x-a)+2a(y-a)=0,即x-2y=-a ①,
得-a(x-a)+2a(y-a)=0,即x-2y=-a ①,
又因为 且
且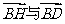 的方向相同,
的方向相同,
故 ,即2x+y=2a
,即2x+y=2a
由①②解得
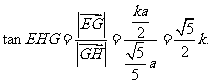
由k>0知∠EHG是锐角,由∠EHG>30º,得tanEHG>tan30º,即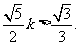 …12分
…12分
18.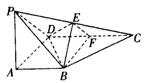 (
( 本小题满分12分)
本小题满分12分)
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB=90º,AB//CD,AD=CD=2AB,E、F分别为PC、CD的中点.
⑴证明:CD⊥平面BEF;
⑵设PA=k·AB且二面角E-BD-C的平面角大于30º,求k的取值范围.
17.(本小题满分12分)
某篮球职业联赛的总决赛在甲队与乙队间角逐,采用五局三胜制,即若一队先胜三场,则此队获胜,比赛结束,雅创教育网因两队实力相当,每场比赛获胜的可能性相等,据以往资料统计,第一场比赛组织者可获门票收入30万元,以后每场比赛门票收入都比上一场增加10万元,问:
⑴组织者在此次总决赛中获得门票收入不少于180万元的概率是多少?
⑵用 表示组织者在此次总决赛中的门票收入,求
表示组织者在此次总决赛中的门票收入,求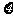 的数学期望?
的数学期望?
解:⑴每场比赛的门票收入构成等差数列{an},其中a1=30,d=10,
Sn=5n2+25n
令Sn≥180,即5n2+25n≥180,解得n≥4或n≤-9(舍)
∴n=4或5
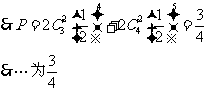 …………………………………………………6分
…………………………………………………6分
⑵
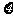 |
120 |
180 |
250 |
|
P |
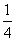 |
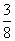 [来源:] [来源:] |
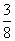 |
∴E =
=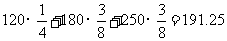 …………………………………………12分
…………………………………………12分
16.(本小题满分12分)
已知△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若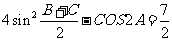 ,
,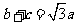 ,求A、B、C的大小.
,求A、B、C的大小.
解: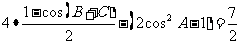

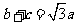 ,由正弦定理得:
,由正弦定理得: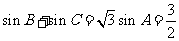
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com