
6.对数运算常用公式
(1)a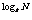 =N
=N
(2)logaM+logaN=loga(MN)
(3)logaM-logaN=loga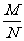
(4)logaMn=nloga|M|
(5)loga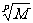 =
= loga|M|
loga|M|
(6)loga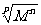 =
=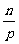 loga|M|
loga|M|
(7)logbM=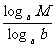
(8)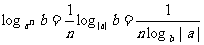
(9)logab·logbc=logac
5.幂函数、指数函数、对数函数的性质
(1)幂函数y=xn(n∈Q)的性质
①当n>0时,函数图像过点(1,1),(0,0),且在第一象限内随x增加,图像上升;
②当n<0时,函数图像过点(1,1),且在第一象限内随x增加,图像下降。
(2)指数函数和对数函数性质表:
|
|
指数函数 |
对数函数 |
|
图像 |
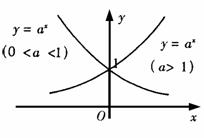 |
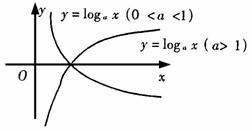 |
|
性质 |
定义域R,值域(0,+∞),过点(0,1)。当a>1时,在R上是增函数。当0<a<1时,在R上是减函数。 |
定义域(0,+∞),值域R,过点(1,0)。当a>1时,在(0,+ ∞)上是增函数。当0<a<1时,在(0,+ ∞)上是减函数。 |
4.三个“二次”的相关问题
(1)地位作用:
三个“二次”(即一元二次函数、一元二次方程、一元二次不等式)是中学数学的重要内容,具有丰富的内函和密切的联系,同时也是研究包含二次曲线在内的许多内容的工具。高考试题中近一半的试题与这三个“二次”问题有关。
(2)二次函数的基本性质
①二次函数的三种表示法:y=ax2+bx+c;y=a(x-x1)(x-x2);y=a(x-x0)2+n(a≠0);
②当a>0时,f(x)在区间[p,q]上的最大值M,最小值m,令x0= (p+q)。
(p+q)。
若- <p,则f(p)=m,f(q)=M;
<p,则f(p)=m,f(q)=M;
若p≤- <x0,则f(-
<x0,则f(- )=m,f(q)=M;
)=m,f(q)=M;
若x0≤- <q,则f(p)=M,f(-
<q,则f(p)=M,f(- )=m;
)=m;
若- ≥q,则f(p)=M,f(q)=m。
≥q,则f(p)=M,f(q)=m。
(3)二次方程的实根分布条件:
①二次方程f(x)=0的两根中一根比r大,另一根比r小 a·f(r)<0;
a·f(r)<0;
②二次方程f(x)=0的两根都大于r
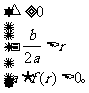
③二次方程f(x)=0在区间(p,q)内有两根

④二次方程f(x)=0在区间(p,q)内只有一根 f(p)·f(q)<0,或
f(p)·f(q)<0,或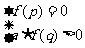 (检验)或
(检验)或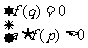 (检验)。
(检验)。
⑤二次方程f(x)=0的一根小于p,另一根大于q(p<q)
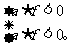
(4)二次不等式的转化策略:
①二次不等式f(x)≤0的解集是:(-∞,α ∪[β,+∞
∪[β,+∞
 a<0且f(α)=f(β)=0.
a<0且f(α)=f(β)=0.
②当a<0时,f(α)<f(β)  |α+
|α+ |>|β+
|>|β+ |;
|;
当a>0时,f(α)<f(β)  |α+
|α+ |<|β+
|<|β+ |。
|。
③当a>0时,二次不等式f(x)>0在[p,q]上恒成立
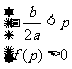 或
或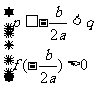 或
或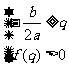
④f(x)>0恒成立
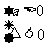 或
或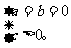
f(x)<0恒成立
 或
或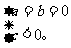
3.函数的性质
(1)函数的概念:定义域、值域、对应法则、反函数、复合函数、分段函数;
(2)函数的性质:单调性、奇偶性、有界性、极(最)值性、对称性、周期性等;
(3)函数对称性与周期性的几个结论:
①设函数y=f(x)的定义域为R,且满足条件f(a+x)=f(b-x),则函数y=f(x)的图像关于直线x=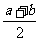 对称;
对称;
②定义在R上的函数y=f(x)对定义域内任意x有f(x+a)=f(x-b),则y=f(x)是以T=a+b为周期的函数;
③定义在R上的函数y=f(x)对定义域内任意x满足条件f(x)=2b-f(2a-x),则y=f(x)关于点(a,b)对称;
④若y=f(x)既关于直线x=a对称,又关于x=b(a≠b)对称,则y=f(x)一定是周期函数,且T=2|a-b|是它的一个周期;
⑤若y=f(x)既关于直线x=a对称,又关于点(b,c)中心对称,则y=f(x)一定是周期函数,且T=4|a-b|是它的一个周期。
(4)函数的奇偶性与单调性:
①奇函数与偶函数的定义域关于原点对称,图像分别关于原点与y轴对称;
②任意定义在R上的函数f(x)都可以惟一地表示成一个奇函数与一个偶函数的和。即
f(x)= 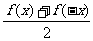 +
+
③若奇函数f(x)在区间[a,b](0≤a<b)上单调递增(减),则f(x)在区间[-b,-a]上也是单调递增(减);
若偶函数f(x)在区间[a,b](0≤a<b)上单调递增(减),则f(x)在区间[-b,-a]上单调递减(增);
④函数f(x)在R上单调递增,若f(a)>f(b),则a>b;
函数f(x)在R上单调递减,若f(a)>f(b),则a<b;
⑤若f(x)在定义域内是增(减)函数,则它的反函数y=f-1(x)在定义域内也是增(减)函数。
2.集合
(1)作用地位
“集合”是数学研究的基本对象之一。学习集合的概念,有助于理解事物的逻辑关系和对应关系,加深对数学的抽象特征的理解,也能提高使用数学语言的能力。
高考试题中,对集合从两个方面进行考查:一方面是考查对集合概念的认识和理解水平,主要表现在对集合的识别和表达上。如对集合中涉及的特定字母和符号,元素与集合间的关系,集合与集合间的比较,另一方面,则是考查学生对集合知识的应用水平,如求方程组、不等式组及联立条件组的解集,以及设计、使用集合解决问题等。
(2)重点与难点
重点是集合的概念和表示法及交、并、补集的运算。难点是集合运算的综合运用,特别是带有参数的不等式解集的讨论。
(3)有关子集的几个等价关系
①A∩B=A A
A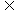 B;
B;
②A∪B=B A
A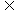 B;
B;
③A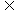 B
B C uA
C uA C uB;
C uB;
④A∩CuB
=
 CuA
CuA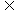 B;
B;
⑤CuA∪B=I A
A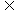 B。
B。
(4)交、并集运算的性质
①A∩A=A,A∩ =
= ,A∩B=B∩A;
,A∩B=B∩A;
②A∪A=A,A∪ =A,A∪B=B∪A;
=A,A∪B=B∪A;
③Cu (A∪B)= CuA∩CuB,Cu (A∩B)= CuA∪CuB;
(5)有限子集的个数:设集合A的元素个数是n,则A有2n个子集,2n-1个非空子集。
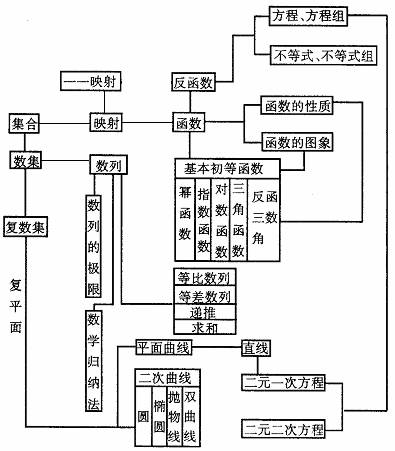
1.函数及相关知识关系表
7.掌握指数函数、对数函数的概念及其图像和性质,并会解简单的指数方程和对数方程。
6.理解对数的概念,掌握对数的性质。
5.理解分数指数幂、根式的概念,掌握分数指数幂的运算法则。
4.理解函数的单调性和奇偶性的概念,并能判断一些简单函数的单调性和奇偶性。能利用函数的奇偶性来描绘函数的图像。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com