
1.当地球由④点公转到⑤点的过程中( )
A.公转速度逐渐变小 B.公转速度逐渐变大
C.南极圈内极昼范围逐渐增大 D.北半球各地白昼不断变长
20. (本小题满分16分)
已知函数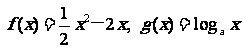 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果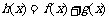 是增函数,且
是增函数,且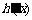 存在零点(
存在零点(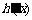 为
为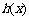 的导函数).
的导函数).
(Ⅰ)求a的值;
(Ⅱ)设A(x1,y1)、B(x2,y2)(x1<x2)是函数y=g(x)的图象上两点,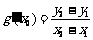 (
(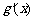 为
为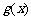 的导函数),证明:
的导函数),证明: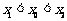 .
.
“金太阳”江苏省2010年百校大联考
19. (本小题满分16分)
已知圆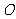 :
: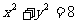 交
交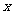 轴于
轴于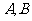 两点,曲线
两点,曲线 是以
是以 为长轴,直线:
为长轴,直线: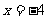 为准线的椭圆.
为准线的椭圆.
 (1)求椭圆的标准方程;
(1)求椭圆的标准方程;
(2)若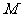 是直线上的任意一点,以
是直线上的任意一点,以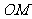 为直径的圆
为直径的圆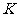 与圆
与圆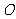 相交于
相交于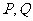 两点,求证:直线
两点,求证:直线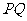 必过定点
必过定点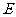 ,并求出点
,并求出点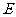 的坐标;
的坐标;
(3)如图所示,若直线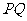 与椭圆
与椭圆 交于
交于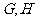 两点,且
两点,且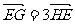 ,试求此时弦
,试求此时弦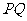 的长.
的长.
18. (本小题满分16分)
某水库堤坝因年久失修,发生了渗水现象,当发现时已有200m2的坝面渗水.经测算知渗水现象正在以每天4m2的速度扩散.当地政府积极组织工人进行抢修.已知每个工人平均每天可抢修渗水面积2m2,每人每天所消耗的维修材料费75元,劳务费50元,给每人发放50元的服装补贴,每渗水1m2的损失为250元.现在共派去x名工人,抢修完成共用n天.
(Ⅰ)写出n关于x的函数关系式;
(Ⅱ)要使总损失最小,应派去多少名工人去抢修(总损失=渗水损失+政府支出).
17. (本小题满分14分)
已知数列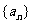 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足
(1)求数列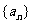 的通项公式;
的通项公式;
(2)数列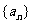 和数列
和数列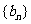 满足等式
满足等式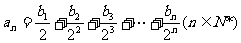 ,求数列
,求数列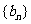 的前n项和Sn。
的前n项和Sn。
16. (本小题满分14分)
 已知直三棱柱
已知直三棱柱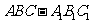 中,
中,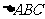 为等腰直角三角形,
为等腰直角三角形,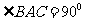 ,且
,且 ,
,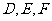 分别为
分别为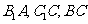 的中点,
的中点,
(1)求证: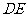 //平面
//平面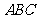 ;
;
(2)求证: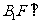 平面
平面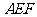 ;
;
(3)求三棱锥E-AB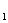 F的体积。
F的体积。
15. (本小题满分14分)
已知函数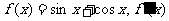 是
是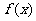 的导函数。
的导函数。
(Ⅰ)求函数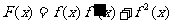 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)若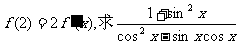 的值。
的值。
14. 在实数数列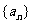 中,已知
中,已知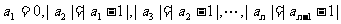 则
则 的最大值为
▲ .
的最大值为
▲ .
13. 已知向量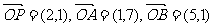 ,设M是直线OP上任意一点(O为坐标原点),则
,设M是直线OP上任意一点(O为坐标原点),则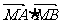 的最小值为 ▲ .
的最小值为 ▲ .
12. 设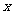 、
、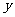 满足约束条件
满足约束条件 若目标函数为
若目标函数为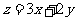 ,则
,则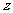 的最大值为
的最大值为
▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com