
教学中重视知识的形成过程的教学,使学生在掌握知识的思维实践中既获得了识, 得到思维训练。学生往往认为学习定义,定理,公式等只要记着就行了,对定理的证明,公式的推导很少能给以足够的重视;教师也往往只重视让学生把定义,定理,公式正确地,全面地接受下来,而不去探讨它们的由来和实质,课堂上认真地,严格地对每一个定理加以证明,对每一个公式给以推导,忽略证明和推导的原因。这样学生只会机械的记公式,套定理,而会忽视了运用的前提,条件。例如,求数列1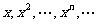 的前n项和,学生会毫不犹豫地应用等比数列前项和公式
的前n项和,学生会毫不犹豫地应用等比数列前项和公式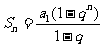 ,得出结果
,得出结果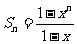 。其一,忽视该公式应用的条件
。其一,忽视该公式应用的条件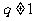 ,而在本题中公比q有可能为1,此时,得到一常数列,其前项和是
,而在本题中公比q有可能为1,此时,得到一常数列,其前项和是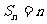 ;其二,忽视等比数列的条件:等比数列中,其公比和数列中的项不可能为0,而本题中x可以为0,得数列1,0,0,---,其前n项和
;其二,忽视等比数列的条件:等比数列中,其公比和数列中的项不可能为0,而本题中x可以为0,得数列1,0,0,---,其前n项和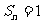 。加深理解“等比数列(公比
。加深理解“等比数列(公比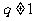 )的前项和公式
)的前项和公式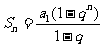 ”后,面临这类问题不会顾此失彼了。还有数列的通项公式
”后,面临这类问题不会顾此失彼了。还有数列的通项公式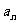 与前项和公式
与前项和公式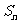 的关系:
的关系: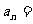 {
{
 n=1,很多学生也只是勉强记忆,其实只要回归
n=1,很多学生也只是勉强记忆,其实只要回归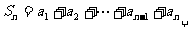 就很明了清晰了。
就很明了清晰了。
一,精心设计课堂教学,用连系的方法教学,同时,训练学生的思维。
我们说一个稍微用功的学生,在课堂上听懂教师讲的课并不难,仿照例题解几道题也完全可以,但是要用学过的知识去解决一个新的问题就不是轻而易举的了。故必须放弃“前提--结论”式的教学,而用以思维为主流,以链结式的学生的思路展开。 例数列概念一节的教学,概念较多。如不注重思维引导,只顾孤立地呈现,学生是必会象猴子下山,摘了西瓜,丢了芝麻,也可能会有似象非象之感,我在教学中按下面的方式进行,比较适当。先由集合的概念→ 引入数列概念→ 列举出课本中的几个数列→ 对比集合的特点→ 结合实例归纳出数列的特点→对比集合中的元素→ 引出数列中的项→ 由此得出其序号→ 由序号与项的对应→ 联想到映射→ 一一映射,函数→ 数列与其序号构成一个函数→ 联想到函数的定义域→ 它的定义域是正整数集或它的一个子集→ 有限数列,无限数列,即数列的分类;函数→ 函数的图象→ 由定义域的特性,得出是一群孤立的点;函数→ 函数解析式→ 通项公式概念→ 分析出一个简单数列的通项公式→ 由通项公式写出数列中的前几项→ 看事实,悟规律→ 由前几项写出一个通项公式,(有的可写出不只一个通项公式,有的却写不出通项公式)整个过程都是联系对比所学知识,很自然引出新的问题,既突出了重点,又化解了难点,并且把所有知识一串而成。真可谓一气哈成。
二,数学的综合运用上,应顺应学生的思维去挖掘,而不是强加给学生以解题模式,框架,束缚学生的思维,让他们自己去感受,去体会,去领悟,例题的讲解追求的不是解题过程写得多么详细,而是解题的思维过程,这样学生才不会单纯摹仿,不会缺乏独立分析问题的能力,遇到新问题不会觉得束手无策。例设{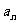 }的前项和S
}的前项和S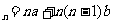 (n=1,2,---),a ,b是常数,且b
(n=1,2,---),a ,b是常数,且b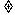 0 。
0 。
(1),证明{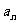 }是等到差数列;
}是等到差数列;
(2),证明以(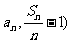 为坐标的点
为坐标的点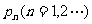 都落在同一条直线上,并写出此直线的方程。
都落在同一条直线上,并写出此直线的方程。
分析并推导:要证明数列{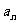 }是一等差数列,就是要得出
}是一等差数列,就是要得出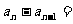 常数,此时显然要求出
常数,此时显然要求出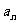 的通式,而
的通式,而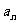 可由
可由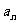 =
= 得,
得,
故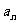 =
= =
=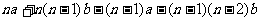 =---=
=---=
此时猛然发现这里n只能取的数 ,这样得到的是通项中从第二项开始后各项,那么首项到哪里去找呢?噢,原来在用
,这样得到的是通项中从第二项开始后各项,那么首项到哪里去找呢?噢,原来在用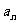 =
= 时就忽略了条件
时就忽略了条件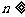 2,而由
2,而由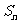 得
得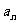 本身就还包含着
本身就还包含着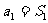 这样一个“始祖”。是以学生自然补充这一点,并验证
这样一个“始祖”。是以学生自然补充这一点,并验证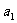 符合
符合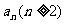 ,最后由前述分析,得证。整个过程做到让学生自己去发现问题,自己去寻找答案。针对第二个问题,学生开始也是感到非常棘手的。首先是从知识结构上,一下子就从数列跳到畏难的平面解析几何;第二要证明的点不是一个,二个或多个具体的点在一条直线上,而是无数个抽象的点。显而易见,不可能一个,一个去求,只有寻找某个规律性的东西才行。回到具体的坐标点,细思量,发现至少可以确定第一个点(
,最后由前述分析,得证。整个过程做到让学生自己去发现问题,自己去寻找答案。针对第二个问题,学生开始也是感到非常棘手的。首先是从知识结构上,一下子就从数列跳到畏难的平面解析几何;第二要证明的点不是一个,二个或多个具体的点在一条直线上,而是无数个抽象的点。显而易见,不可能一个,一个去求,只有寻找某个规律性的东西才行。回到具体的坐标点,细思量,发现至少可以确定第一个点(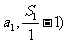 ,即(
,即(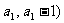 ,其他的点呢确实不好找了,这时,可先放一放,回到如何证明点共线的问题,是要得出每两点所确定直线的斜率相等。如此,我们要求多少个斜率,用组合数来求要有个。似乎走到了一个死胡同-----,规律是什么?不就是很多归结为一个吗。这里的无数个点能否用一个点表示呢。这不就是通式(
,其他的点呢确实不好找了,这时,可先放一放,回到如何证明点共线的问题,是要得出每两点所确定直线的斜率相等。如此,我们要求多少个斜率,用组合数来求要有个。似乎走到了一个死胡同-----,规律是什么?不就是很多归结为一个吗。这里的无数个点能否用一个点表示呢。这不就是通式(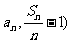 吗?对呀!然后它(们)与第一个点所确定直线的斜率是一个固定的,即为一常数。问题终于豁然开朗。峰回路转,有学生发问,这里用到求斜率,那它是否有斜率呢?题目中并没有指明。对,那什么情况下没有斜率呢?当两点的横坐标相同时,所确定的直线不存在斜率。这里的横坐标
吗?对呀!然后它(们)与第一个点所确定直线的斜率是一个固定的,即为一常数。问题终于豁然开朗。峰回路转,有学生发问,这里用到求斜率,那它是否有斜率呢?题目中并没有指明。对,那什么情况下没有斜率呢?当两点的横坐标相同时,所确定的直线不存在斜率。这里的横坐标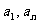 会相等吗?即数列{
会相等吗?即数列{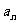 }是常数列吗?前面
}是常数列吗?前面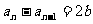 ,由条件
,由条件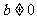 知数列不是常数列。由此尽管题目所涉及的内容不少,分支及要注重的环节较多,但只要能做到用“理”去服题,总是可以跨越的。
知数列不是常数列。由此尽管题目所涉及的内容不少,分支及要注重的环节较多,但只要能做到用“理”去服题,总是可以跨越的。
三,培养学生抓住问题的实质
数学教学并非解题教学,解题只是手段,重要的是通过解题教会学生思维,提高学生的能力。关键是努力提高每一道题的功效性,在错综纷杂的题型,套路中领略其万变不离其宗的实质,以不变应变的策略,找出解题的思想方法,支解简化各环节,例,对于二次函数结合对数函数,指数函数的复合,更配以绝对值,或需考虑移轴的方面,来寻求函数的单调性,值域,------,下表得以解决:
 |
|
|
|
|
|
|
|
图象 |
|
|
|
|
|
|
|
|
定义域 |
|
|
|
{x|x>-1} |
|
|
|
|
值域 |
|
R |
|
|
|
|
|
|
增区间 |
|
|
(0、+ ) |
|
|
|
|
|
函数 |
|
|
|
|
|
|
|
增区间 |
|
|
|
(-2、1] |
|
|
|
减区间 |
|
|
[-2、1] |
|
|
|
|
值域 |
|
(0、2 ] |
|
|
|
|
|
定义域 |
[-2、4] |
|
|
|
|
|
四,注重学生形象思维的能力的培养。
思维能力不仅指抽象的逻辑思维,也包括着蕴含“轻捷灵活”的形象思维,即常说的数形结合思想,上面第四点的实例已把它演绎得淋漓尽致。再例对于等差数列前n项和公式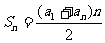
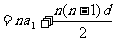
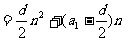 ,是关于n的不含常数项的二次函数,对应的图象是一过原点的抛物线,
,是关于n的不含常数项的二次函数,对应的图象是一过原点的抛物线,
故由其特性,若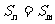 ,可知:
,可知:
(1),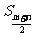 取最大值(或最小值)(若为m+n奇数,取接近的相邻的整数);
取最大值(或最小值)(若为m+n奇数,取接近的相邻的整数);
(2),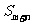 为0。
为0。
总之,加强引导学生思维 ,鼓励创新。益,是深远的。
23.(本题满分20分,第1小题6分,第2小题6分,第3小题8分)
对于定义在D上的函数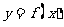 ,若同时满足
,若同时满足
(I)存在闭区间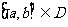 ,使得任取
,使得任取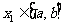 ,都有
,都有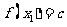 (
(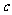 是常数);
是常数);
(II)对于D内任意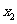 ,当
,当 时总有
时总有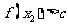 称
称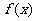 为“平底型”函数。
为“平底型”函数。
(1)判断 ,
,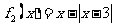 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;
(2)设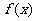 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若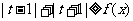 ,对一切
,对一切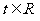 恒成立,求实数
恒成立,求实数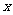 的范围
的范围
(3)若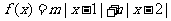 是“平底型”函数,求
是“平底型”函数,求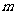 和
和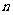 满足的条件
满足的条件
22.(本题满分16分,第1小题3分,第2小题8分,第3小题5分)
已知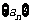 是公差为
是公差为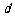 的等差数列,它的前
的等差数列,它的前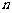 项和为
项和为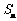 , 等比数列
, 等比数列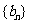 的前
的前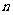 项和为
项和为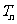 ,
,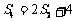 ,
,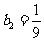 ,
,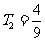
(1)求公差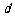 的值;
的值;
(2)若对任意的 ,都有
,都有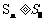 成立,求
成立,求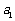 的取值范围
的取值范围
(3)若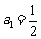 ,判别方程
,判别方程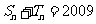 是否有解?说明理由国
是否有解?说明理由国
21.(本题满分15分,第1小题8分,第2小题7分)
据行业协会预测:某公司以每吨10万元的价格销售某种化工产品,可售出该产品1000吨,若将该产品每吨的价格上涨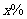 ,则销售量将减少
,则销售量将减少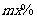 ,且该化工产品每吨的价格上涨幅度不超过
,且该化工产品每吨的价格上涨幅度不超过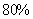 ,(其中
,(其中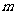 为正常数)
为正常数)
(1)当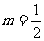 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
(2)如果涨价能使销售总金额比原销售总金额多,求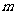 的取值范围.
的取值范围.
20.(本题满分15分,第1小题5分,第2小题5分,第3小题5分)
如图:直三棱柱 内接于高为
内接于高为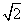 的圆柱中,已知
的圆柱中,已知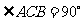 ,
,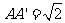 ,
,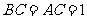 ,
,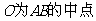
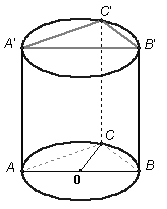 求(1)圆柱的全面积
求(1)圆柱的全面积
(2)求异面直线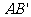 与
与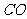 所成的角的大小
所成的角的大小
(3)求直线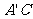 与平面
与平面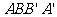 所成的角的大小
所成的角的大小
19.(本题满分12分,第1小题4分,第2小题8分)
如图A.B是单位圆O上的点,且点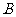 在第二象限. C是圆O与
在第二象限. C是圆O与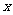 轴正半轴的交点,
轴正半轴的交点,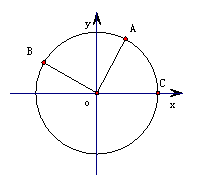 A点的坐标为
A点的坐标为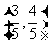 ,△
,△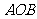 为直角三角形.
为直角三角形.
(1)求 ;
;
(2)求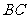 的长度
的长度
18.在等差数列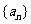 中,若
中,若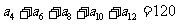 ,则
,则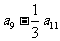 的值为 ( )
的值为 ( )
A.14 B.15 C.16 D.17
17.若不等式f(x)= >0的解集
>0的解集 ,则函数y=f(-x)的图象为
,则函数y=f(-x)的图象为
( )
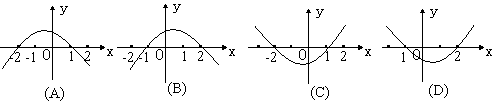
16.设函数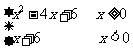 则不等式
则不等式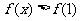 的解集是 ( )
的解集是 ( )
A.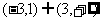 B.
B.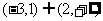
C.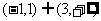 D.
D.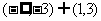
15.在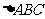 中,“
中,“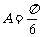 ”是“
”是“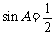 ”的
( )
”的
( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com