
第一节 单项填空(共20小题; 每小题1分, 满分20分)
从各题所给的四个选项(A、B、C和D), 选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21. Teenagers _______ their health because they play computer games too much.
A. damaged B. have damaged C. will damage D. are damaging
22. 设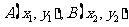 是椭圆
是椭圆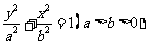 的两点,
的两点,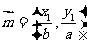 ,
,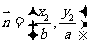 ,且
,且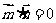 ,椭圆离心率
,椭圆离心率 ,短轴长为2,O为坐标原点。
,短轴长为2,O为坐标原点。
(1)求椭圆方程;
(2)若存在斜率为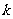 的直线AB过椭圆的焦点
的直线AB过椭圆的焦点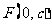 (
(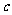 为半焦距),求
为半焦距),求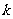 的值;
的值;
(3)试问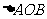 的面积是否为定值?若是,求出该定值;若不是,说明理由。
的面积是否为定值?若是,求出该定值;若不是,说明理由。
福建省厦门外国语学校2010届高三第三次月考
21.(本小题满分13分)某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第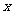 个月的利润
个月的利润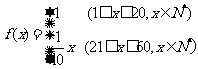 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第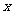 个月的当月利润率
个月的当月利润率 ,例如:
,例如: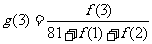 .
.
(1)求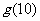 ; (2)求第
; (2)求第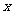 个月的当月利润率
个月的当月利润率 ;
;
(3)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
20. 已知直三棱柱
已知直三棱柱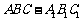 中,
中,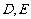 分别为
分别为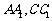 的中点,
的中点,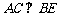 ,点
,点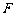 在线段
在线段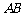 上,且
上,且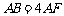 .
.
⑴求证: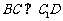 ;
;
⑵若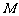 为线段
为线段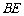 上一点,试确定
上一点,试确定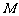 在线段
在线段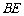 上的位置,
上的位置,
使得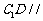 平面
平面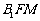 .
.
19. 下表为某班英语及数学成绩分布,全班共50人,成绩分为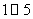 五个档次,例如表中所示英语成绩为4分数学成绩为2分的共5人,设
五个档次,例如表中所示英语成绩为4分数学成绩为2分的共5人,设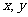 分别表示英语和数学成绩;
分别表示英语和数学成绩;
(1)分别求出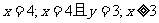 三个事件的概率;
三个事件的概率;
(2)求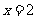 时的概率并求
时的概率并求 的值。
的值。
 |
数学 |
|||||
|
5 |
4 |
3 |
2 |
1 |
||
|
英语 |
5 |
1 |
3 |
1 |
0 |
1 |
|
4 |
1 |
0 |
7 |
5 |
1 |
|
|
3 |
2 |
1 |
0 |
9 |
3 |
|
|
2 |
1 |
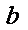 |
6 |
0 |
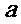 |
|
|
1 |
0 |
0 |
1 |
1 |
3 |
18.(本小题满分12分)已知函数 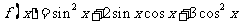 .
.
(1)求函数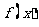 图象的对称中心的坐标;
图象的对称中心的坐标;
(2)求函数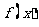 的最大值,并求函数
的最大值,并求函数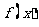 取得最大值时x的值;
取得最大值时x的值;
(3)求函数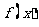 的单调递增区间.
的单调递增区间.
17. 已知数列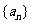 是首项1,公比为q (q>0)的等比数列,并且2a
是首项1,公比为q (q>0)的等比数列,并且2a ,
,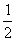 a
a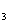 , a
, a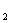 成等差数列.
成等差数列.
(Ⅰ)求q的值 ;(Ⅱ)若数列{b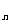 }满足b
}满足b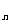 =a
=a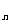 +n, 求数列{b
+n, 求数列{b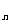 }的前n项和T
}的前n项和T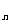 .
.
16. 若数列{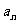 }满足
}满足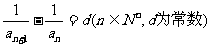 ,则数列{
,则数列{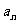 }为“调和数列”,已知数列{
}为“调和数列”,已知数列{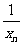 }为“调和数列”,且
}为“调和数列”,且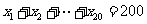 ,则
,则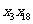 的最大值是_______。
的最大值是_______。
三解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算过程)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com