2．如图所示，闭合矩形铜框的两条长边与一闭合圆环相切，环可沿矩形框的长边滑动，整个装置处于匀强磁场中，当环沿框的长边向右做匀速运动时，则　

A．因铜框所围面积的磁通量不变化，铜框上无电流　

B．因圆环所围面积的磁通量不变化，圆环上无电流　

C．各部分导线内均有电流　

D．各部分导线内均无电流　

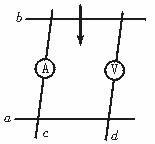[解析] 由于闭合圆环向右移动，egf和ehf等效为两个并联的电源，而eadf和ebcf为两段并联的电阻作为外电路，所以各部分都有电流．　

[答案] C

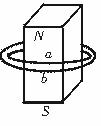
1．如图所示，两同心圆环a和b，处在同一平面内，a的半径小于b的半径，条形磁铁的轴线与圆环平面垂直．则穿过两圆环的磁通量Φ_a与Φ_b的大小关系为　

A．Φ_a＞Φ_b B．Φ_a＜Φ_b　

C．Φ_a＝Φ_b D．无法比较　

[解析] 圆环b的半径大于环a的半径，由于Φ＝Φ_内－Φ_外(其中Φ_内为磁铁内部的磁通量，Φ_外为磁铁外部穿过线圈的磁通量)，故其包含磁铁的外磁场范围越大，则合磁通量越小．(磁铁内部、外部的磁通量方向相反，可抵消)．　

[答案] A　

3、力学与电磁磁应的综合应用

解决这类问题一般分两条途径:一是注意导体或运动电荷在磁场中的受力情况分析和运动状态分析;二是从动量和功能方面分析,由有关的规律进行求解

[例9]如图所示，闭合金属环从高h的曲面滚下，又沿曲面的另一侧上升，整个装置处在磁场中，设闭合环初速为零，摩擦不计，则

　 A．若是匀强磁场，环滚的高度小于h

　 B．若是匀强磁场，环滚的高度等于h

C、若是非匀强磁场，环滚的高度小于h。

D、若是非匀强磁场，环滚的高度大于h。

解析：若是匀强磁场，当闭合金属环从高h的曲面滚下时，无电磁感应现象产生．根据机械能守恒，环滚的高度等于h；若是非匀强磁场，当闭合金属环从高h的曲面滚下时，有电磁感应现象产生，而产生电磁感应的原因是环的运动，所以电磁感应现象所产生的结果是阻碍环的运动，所以环上升的高度小于h，故本题正确答案为B、C

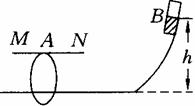[例10]如图所示，光滑弧形轨道和一足够长的光滑水平轨道相连，水平轨道上方有足够长的光滑绝缘杆MN，上挂一光滑铝环A,在弧形轨道上高为h的地方无初速度释放磁铁B(可视为质点)，B下滑至水平轨道时恰好沿A的中心轴线运动，设A,B的质量为M_A.M_B，求A获得的最大速度和全过程中A获得的电能．(忽略B沿弧形轨道下滑时环A中产生的感应电流)

解析：由B下落时只有重力做功可求得B滑至水平轨道的速度值,B沿A环轴线运动时,A内产生感应电流，与B产生相互作用，进入时相互排斥，故v_B减小，v_A增大，B的中点过A环后，AB相互吸引，v_B仍减小，v_A增大；当两者相对静止时，相互作用消失，此时v_A=vB,A其有最大速度．全过程能量守恒,B初态的重力势能转化为AB的动能和A获得的电能．

　　 设B滑至水平轨道的速度为V₁，由于B的机械能守恒，有M_Bgh=½M_B V₁²

　　 所以

　　 设AB最后的共同速度为V₂，由于轨道铝环和杆均光滑，对系统有： M_Bv₁=(M_A+M_B)v₂

　　 所以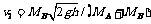

　　 V₂即为所求的A获得的最大速度．又根据能量守恒有：M_Bgh=½(M_A+M_B)v₂²+E_电

所以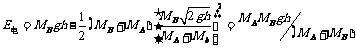

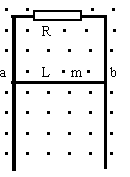
[例11].竖直放置的U形导轨宽为L，上端串有电阻R(其余电阻不计)。磁感应强度为B的匀强磁场方向向外。金属棒ab质量为m，与导轨接触良好，不计摩擦，从静止释放后保持水平而下滑。求其下滑的最大速度。

分析：释放后，随着速度的增大，感应电动势E、感应电流I、安培力F都随之增大，当F=mg时，加速度变为零，达到最大速度。。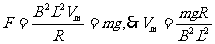

*注意该过程中的能量转化：重力做功的过程是重力势能向其他能转化的过程；安培力做功的过程是机械能向电能转化的过程；然后电流做功的过程是电能向内能转化的过程。稳定后重力的功率等于电功率也等于热功率。

*如果在该图上端电阻右边安一只电键，让ab下落一段距离后再闭合电键，那么闭合电键后ab的运动情况如何？(无论何时闭合电键，ab可能先加速后匀速，也可能先减速后匀速，但最终稳定后的速度都一样)。

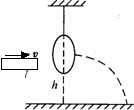[例12]如图所示，质量为100 g的铝环，用细线悬挂起来，环中央距地面h为0. 8 m.有一质量200 g的磁铁以10 m/s的水平速度射入并穿过铝环，落在距铝环原位置水平距离3.6 m处，则在磁铁与铝环发生相互作用时：

(1)铝环向哪边偏斜？它能上升多高？

(2)在磁铁穿过铝环的整个过程中，环中产生了多少电能？

解析:(1)环向右偏斜，令铝环质量m1 = 0. 1 kg, 磁铁质量m2=0. 2 kg

磁铁做平抛运动;s = 3. 6＝vt,又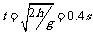,v＝9 m/s

又：磁铁与铝环作用时水平方向的动量守恒m2v0=m2v+m1v1,v1=2 rn/s

则：环：m1gH＝½m1v12;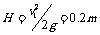

　(2)环中产生的电能为系统的机械能损失：E电＝△E＝½m2v02一½m2v2一½m1v12=1.7(J)

试题展示

2、公式E=BLVsinθ与E=nΔΦ/Δt的区别

(1)区别：一般来说，E=nΔΦ/Δt求出的是Δt时间内的平均感应电动势，E与某段时间或某个过程相对应;E= BLvsin θ求出的是瞬时感应电动势,E与某个时刻或某个位置相对应．

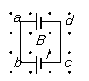另外, E=nΔΦ/Δt求得的电动势是整个回路的感应电动势，而不是回路中某部分导体的电动势，整个回路的感应电动势为零时，其回路中某段导体的感应电动势不一定为零．

如图所示，正方形导线框abcd垂直于磁感线在匀强磁场中匀速向下运动时，由于ΔΦ/Δt=0，故整个回路的感应电动势E=0，但是ad和bc边由于做切割磁感线运动，仍分别产生感应电动势Ead=Ebc=BLv,对整个回路来说，Ead和Ebc方向相反，所以回路的总电动势E=0，感应电流也为零．虽然E=0，但仍存在电势差，Uad=Ubc=BLv,相当于两个相同的电源ad和bc并联．

(2)联系：公式①E=nΔΦ/Δt和公式②E=BLVsinθ是统一的，当①中的Δt→0时，则E为瞬间感应电动势．只是由于高中数学知识所限我们还不能这样求瞬时感应电动势．公式②中的v若代入平均速度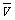，则求出的E为平均感应电动势，实际上②式中的L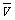sinθ=△S/Δt，所以公式E=BL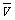sinθ=B△S/Δt.只是一般来说用公式E=nΔΦ/Δt求平均感应电动势更方便，用E= BLvsinθ求瞬时感应电动势更方便．

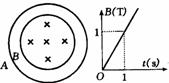[例7]如图所示，AB是两个同心圆，半径之比R_A∶R_B=2∶1，AB是由相同材料，粗细一样的导体做成的，小圆B外无磁场，B内磁场的变化如图所示，求AB中电流大小之比(不计两圆中电流形成磁场的相互作用)．

　解析：在ε=ΔB/Δt·S中，S是磁场变化的面积．所以I_A=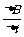·．I_B=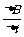·,　　　 所以I_A∶I_B＝1∶2

注意:IA的计算不可用做实际面积大小,写成I_A=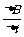·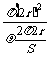,而得到I_A∶I_B＝2∶1的错误结论

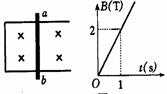[例8]如图所示，光滑导轨宽0.4 m，ab金属棒长0.5m，均匀变化的磁场垂直穿过其面，方向如图，磁场的变化如图所示，金属棒ab的电阻为1Ω，导轨电阻不计，自t＝0时，ab棒从导轨最左端，以v＝1m/s的速度向右匀速运动，则( AB　　　 )

　　 A．1s末回路中的电动势为1．6V

　　 B．1s末棒ab受安培力大小为1．28N

　　 C．1s末回路中的电动势为0．8V

　　 D．1s末棒ab受安培力大小为0．64N

解析：这里的ΔΦ变化来自两个原因，一是由于B的变化，二是由于面积S的变化，显然这两个因素都应当考虑在内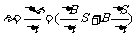．， ΔB/Δt=2T/S，ΔS/Δt=VLΔt=2×1×0．4＝0.8 m

　　 1秒末B=2T，ΔS/Δt=0．4m²／s，　 所以ε＝(+)=1.6V

　　 回路中电流I＝ε/R=1.6／1A＝1.6A,　　 安培力F＝BIl＝2×1.6×0．4N＝1.28N

(2)当线圈是N匝时则电量为：Q=NΔΦ/R

　如图所示，当磁铁完全插入时，假设线圈中磁通量变化为ΔΦ，通过每匝线圈磁通量变化与N匝线圈的磁通量变化一样都为ΔΦ；通过每匝线圈磁通量的变化率都为ΔΦ/Δt，因为是N匝，相当于N个相同电源串联，所以线圈的感应电动势ε＝Nε₀=N ΔΦ/Δt．

(3)如图所示，磁铁快插与慢插两情况通过电阻R的电量一样，但两情况下电流做功及做功功率不一样．　　

[例5].长L₁宽L₂的矩形线圈电阻为R，处于磁感应强度为B的匀强磁场边缘，线圈与磁感线垂直。将线圈以向右的速度v匀速拉出磁场，求：①拉力F大小；②拉力的功率P；③拉力做的功W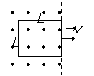；④线圈中产生的电热Q；⑤通过线圈某一截面的电荷量q。

解析：特别要注意电热Q和电荷q的区别，其中 q与速度无关！

规律方法

1、Φ、ΔΦ、ΔΦ/Δt三个概念的区别

磁通量Ф=BScosθ，表示穿过这一平面的磁感线条数；磁通量的变化量△Ф=Ф₂－Ф₁表示磁通量变化的多少；磁通量的变化率ΔФ/Δt表示磁通量变化的快慢. Ф大,ΔФ及ΔФ/ΔT不一定大, ΔФ/ΔT大，Ф及ΔФ也不一定大．它们的区别类似于力学中的v. ΔV及a=ΔV/△t的区别.

[例6]长为a宽为b的矩形线圈，在磁感强度为B的匀强磁场中垂直于磁场的OO′轴以恒定的角速度ω旋转，设t= 0时，线圈平面与磁场方向平行，则此时的磁通量和磁通量的变化率分别是 [ 　]

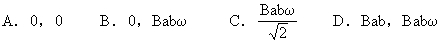
解析:线圈在匀强磁场中绕垂直于磁场的轴转动时，产生交变电动势e=ε_mcosωt = Babωcosωt。当t=0时，cosωt=1，虽然磁通量Ф=0,但电动势有最大值,由法拉第电磁感应定律ε=ΔФ/Δt可知当电动势为最大值时，对应的磁通量的变化率也最大，即ε=(ΔФ/Δt)_max=Babω,正确选项B

(1)定律内容:电路中感应电动势的大小，跟穿过这一电路的磁通量的变化率成正比．ε=nΔφ/Δt

(2)另一种特殊情况:回路中的一部分导体做切割磁感线运动时,其感应电动势ε=BLvsinθ

(3)定律的几种表示式ε=nΔφ/Δt，ε=BLvsinθ，ε=ΔB/Δt·S，ε=½BL²ω；

(4)几点说明:

①这里的变化率应该同变化量区别开，变化量大变化率不一定大，主要是看变化量跟时间比值的大小．即变化率的大小．　

②ε=nΔφ/Δt是定律的表达式，在B不变而面积发生变化时推导出ε=BLvsinθ，当B、l、v三者不垂直或其中的二者不垂直时，乘sinθ即是找出垂直的分量.公式ε=ΔB/Δt·S是在面积不变的情况下磁感应强度发生变化而推出的公式．

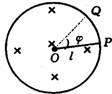
③导出式ε=½BL²ω的推导如下：如图所示，长为l的金属棒在磁感应强度为B的匀强磁场中绕O点以角速度ω转动，设在Δt时间内棒的端点由P运动到Q，则OP两点的电势差ε=Δφ/Δt=BΔS/Δt=B½LPQ/Δt=½BL²ω,这实际上是B不变而面积发生变化的情况，

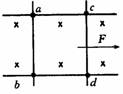[例3]两根平行的长直金属导轨，其电阻不计，导线ab、cd跨在导轨上且与导轨接触良好，如图所示，ab的电阻大于cd的电阻，当d在外力F₁，(大小)的作用下，匀速向右运动时，ab在外力F₂(大小)作用下保持静止，那么在不计摩擦力的情况下(U_ab、U_cd是导线与导轨接触处的电势差)(　　 D　　　 )

　　 A．F₁＞F₂，U_ab＞U_cd　　　 B．F₁＜F₂，U_ab＝U_cd

　　 C．F₁＝F₂，U_ab＞U_cd　　　 D．F₁＝F₂， U_ab=U_cd

解析：通过两导线电流强度一样，两导线都处于平衡状态，则F₁＝BIL，F₂＝BIL，所以F₁＝F₂，因而AB错．对于U_ab与Ucd的比较， U_ab=IR_ab，这里cd导线相当于电源，所以U_cd是路端电压，这样很容易判断出U_cd＝IR_ab 即U_ab＝U_cd．正确答案D

[例4]如图所示，磁场方向与水平而垂直，导轨电阻不计，质量为m长为l，电阻为R的直导线AB可以在导轨上无摩擦滑动从静止开始下滑过程中，最大加速度为　　　 ；最大速度为　　　　 。

解析：ab开始运动的瞬间不受安培力的作用，因而加速度最大，为a=mgsinα/m=gsinα，AB从静止开始运动，于是产生了感应电动势，从而就出现了安培力，当安培力沿斜面分力等于mgsinα时．AB此时速度最大．

对棒受力分析，Fcosα=mgsinα，此时，AB速度最大，而F＝BLI

　　 I=BLvcosα/R，得：v=mgRtgα/ B²L²cosα．

4.产生感应电动势的条件:

无论回路是否闭合,只要穿过线圈的磁通量发生变化,线圈中就有感应电动势产生,产生感应电动势的那部分导体相当于电源.

电磁感应现象的实质是产生感应电动势,如果回路闭合,则有感应电流,如果回路不闭合，则只能出现感应电动势，而不会形成持续的电流．我们看变化是看回路中的磁通量变化，而不是看回路外面的磁通量变化

[例1]线圈在长直导线电流的磁场中，作如图所示的运动：A向右平动；B向下平动，C、绕轴转动(ad边向外)，D、从纸面向纸外作平动，E、向上平动(E线圈有个缺口)，判断线圈中有没有感应电流？

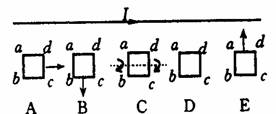解析：A．向右平移，穿过线圈的磁通量没有变化，故A线圈中没有感应电流；B．向下平动，穿过线圈的磁通量减少，必产生感应电动势和感应电流；C．绕轴转动．穿过线圈的磁通量变化(开始时减少)，必产生感应电动势和感应电流；D．离纸面向外，线圈中磁通量减少，故情况同BC；E．向上平移，穿过线圈的磁通量增加，故产生感应电动势，但由于线圈没有闭合电路，因而无感应电流

因此，判断是否产生感应电流关键是分清磁感线的疏密分布，进而判断磁通量是否变化．

答案：BCD中有感应电流

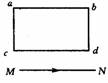
[例2]如图所示，当导线MN中通以向右方向电流的瞬间，则cd中电流的方向(　 B　　 )

　　 A．由 C向d

　　 B．由d向C

　　 C．无电流产生

　　 D．AB两情况都有可能

　解析：当MN中通以如图方向电流的瞬间，闭合回路abcd中磁场方向向外增加，则根据楞次定律，感应电流产生磁场的方向应当垂直纸面向里，再根据安培定则可知， cd中的电流的方向由d到C，所以B结论正确．

3.引起磁通量变化的常见情况

①闭合电路中的部分导线做切割磁感线运动导致Φ变化;

②线圈在磁场中转动导致Φ变化

③磁感应强度随时间或位置变化,或闭合回路变化导致Φ变化

注意: 磁通量的变化，应注意方向的变化，如某一面积为S的回路原来的感应强度垂直纸面向里，如图所示，后来磁感应强度的方向恰好与原来相反，则回路中磁通量的变化最为2BS，而不是零．

2．产生感应电流的条件：闭合回路中磁通量发生变化

1．电磁感应现象

只要穿过闭合回路的磁通量发生变化，闭合回路中就有电流产生，这种利用磁场产生电流的现象叫做电磁感应，产生的电流叫做感应电流．