
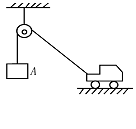
7.如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的受力情况是 A
A.绳的拉力大于A的重力
B.绳的拉力等于A的重力
C.绳的拉力小于A的重力
D.拉力先大于重力,后变为小于重力
6.在抗洪抢险中,战士驾驶摩托艇救人,假设江岸是平直的,洪水沿江向下游流去,水流速度为v1,摩托艇在静水中的航速为v2(v1>v2)。河岸宽度为d,则战士想渡河救人,则摩托艇的
最短距离为 C
A.dv2/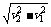
B.0
C.dv1/v2
 D.dv2/v1
D.dv2/v1
5.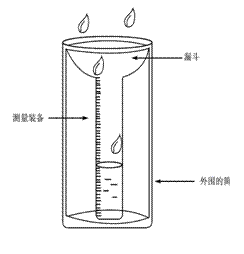 气象测量仪量雨器被认为是最古老的气象仪器,它实际上是一个盛雨的圆筒.如果筒里盛了1
mm水,这表明已降了1 mm的雨,就是如此简单.大多数标准的量雨器都有一个宽漏斗引入圆筒玻璃量杯,而且都有刻度,该仪器可测量低至0.25
mm的降水,图A-4-14-13显示了该标准量雨器.假定雨相对地面以速率v垂直落下,那么用桶盛雨水,在不刮风或有平行于地面的风两种情况下,哪一种能较快地盛满雨水?
气象测量仪量雨器被认为是最古老的气象仪器,它实际上是一个盛雨的圆筒.如果筒里盛了1
mm水,这表明已降了1 mm的雨,就是如此简单.大多数标准的量雨器都有一个宽漏斗引入圆筒玻璃量杯,而且都有刻度,该仪器可测量低至0.25
mm的降水,图A-4-14-13显示了该标准量雨器.假定雨相对地面以速率v垂直落下,那么用桶盛雨水,在不刮风或有平行于地面的风两种情况下,哪一种能较快地盛满雨水?
 [解析]桶中盛的雨水量和桶口面积S,雨水速率v以及时间有关.雨水垂直于地面的速度一定时,刮平行于地面的风时使雨相对于地面的速度(V合)增大.v合=v/cosθ(θ为V合和竖直方向间的夹角).而桶口相对于雨的垂直面积变小了,S’=Scosθ.因此盛满水的时间决定于
V合和S’的乘积,V合S’=VS。两种情况下,如果盛雨水时间相同,所盛雨水量相同。
[解析]桶中盛的雨水量和桶口面积S,雨水速率v以及时间有关.雨水垂直于地面的速度一定时,刮平行于地面的风时使雨相对于地面的速度(V合)增大.v合=v/cosθ(θ为V合和竖直方向间的夹角).而桶口相对于雨的垂直面积变小了,S’=Scosθ.因此盛满水的时间决定于
V合和S’的乘积,V合S’=VS。两种情况下,如果盛雨水时间相同,所盛雨水量相同。
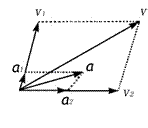
3.关于互成角度的两个初速不为零的匀变速直线运动的合运动,下述说法正确的是( )
A.一定是直线运动
B.一定是曲线运动
C.可能是直线运动,也可能是曲线运动
D.以上都不对
[解析]两个运动的初速度合成、加速度合成如上图所示,当a和v重合时,物体做直线运动,由于题目未给出两个运动的a和v的具体数值,所以以上两种情况都有可能。
2.如图所示,物体作平抛运动的轨迹,在任一点P(x,y)的速度方向的反向延长线交于x轴上的点A,则OA的长为多少?
[解析]设经时间t到达点P,物体作曲线运动,某点的速度方向沿该点切线方向作过点P的切线交x轴于点A,过P作x,y轴的垂线,垂足分别为B、C,由几何图形知AB=y·cotθ
而y=gt2/2,tanθ=vy/vx=gt/v0
 ∴AB=gt2/2×v0/gt=v0t/2=x/2
∴AB=gt2/2×v0/gt=v0t/2=x/2
∴OA=x-AB=x/2.
1.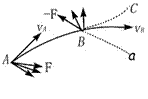 如图所示,物体在恒力F作用下沿曲线从A运动到B,这时突然使它所受的力反向而大小不变(即由F变为-F),在此力作用下,物体以后的运动情况,下列说法正确的是( )
如图所示,物体在恒力F作用下沿曲线从A运动到B,这时突然使它所受的力反向而大小不变(即由F变为-F),在此力作用下,物体以后的运动情况,下列说法正确的是( )
A.物体可能沿曲线Ba运动
B.物体可能沿曲线Bb运动
C.物体可能沿曲线Bc运动
D.物体可能沿原曲线由B返回A
 [解析]物体在A点时的速度
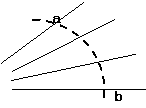
[解析]物体在A点时的速度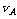 沿A点的切线方向,物体在恒力F作用下沿曲线AB运动,此力F必有垂直于VA的分量,即F力只可能为图A-4-14-6中所示的各种方向之一;当物体到达B点时,瞬时速度vB沿B的切线方向,这时受力F/=-F,即F/只可能为图中所示的方向之一;可知物体以后只可能沿曲线BC运动.
沿A点的切线方向,物体在恒力F作用下沿曲线AB运动,此力F必有垂直于VA的分量,即F力只可能为图A-4-14-6中所示的各种方向之一;当物体到达B点时,瞬时速度vB沿B的切线方向,这时受力F/=-F,即F/只可能为图中所示的方向之一;可知物体以后只可能沿曲线BC运动.
3、曲线运动条件的应用
做曲线运动的物体,其轨迹向合外力所指的一方弯曲,若已知物体的运动轨迹,可判断出合外力的大致方向.若合外力为变力,则为变加速运动;若合外力为恒力,则为匀变速运动;
[例10]质量为m的物体受到一组共点恒力作用而处于平衡状态,当撤去某个恒力F1时,物体可能做( )
A.匀加速直线运动; B.匀减速直线运动;
C.匀变速曲线运动; D.变加速曲线运动。
分析与解:当撤去F1时,由平衡条件可知:物体此时所受合外力大小等于F1,方向与F1方向相反。
若物体原来静止,物体一定做与F1相反方向的匀加速直线运动。
若物体原来做匀速运动,若F1与初速度方向在同一条直线上,则物体可能做匀加速直线运动或匀减速直线运动,故A、B正确。
若F1与初速度不在同一直线上,则物体做曲线运动,且其加速度为恒定值,故物体做匀变速曲线运动,故C正确,D错误。正确答案为:A、B、C。
 [例11]图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a,b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是()
[例11]图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a,b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是()
A.带电粒子所带电荷的符号 B.带电粒子在a,b两点的受力方向
C.带电粒子在a,b两点的速度何处较大 D.带电粒子在a,b两点的电势能何处较大
解析:由图中的曲线可以看出,不管带电粒子由a→b还是由b→a,力的方向必然指向左下方,从而得到正确答案:BCD
思考:若实线为等势线,该题又该如何分析
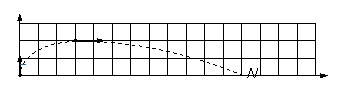 [例12] 如图所示,在竖直平面的xoy坐标系内,oy表示竖直向上方向。该平面内存在沿x轴正向的匀强电场。一个带电小球从坐标原点沿oy方向竖直向上抛出,初动能为4J,不计空气阻力。它达到的最高点位置如图中M点所示。求:
[例12] 如图所示,在竖直平面的xoy坐标系内,oy表示竖直向上方向。该平面内存在沿x轴正向的匀强电场。一个带电小球从坐标原点沿oy方向竖直向上抛出,初动能为4J,不计空气阻力。它达到的最高点位置如图中M点所示。求:
⑴小球在M点时的动能E1。⑵在图上标出小球落回x轴时的位置N。⑶小球到达N点时的动能E2。
解:⑴在竖直方向小球只受重力,从O→M速度由v0减小到0;在水平方向小球只受电场力,速度由0增大到v1,由图知这两个分运动平均速度大小之比为2∶3,因此v0∶v1=2∶3,所以小球在M点时的动能E1=9J。
⑵由竖直分运动知,O→M和M→N经历的时间相同,因此水平位移大小之比为1∶3,故N点的横坐标为12。
⑶小球到达N点时的竖直分速度为v0,水平分速度为2v1,由此可得此时动能E2=40J。
试题展示
2、小船渡河问题分析
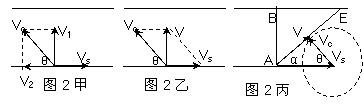 [例9]一条宽度为L的河,水流速度为vs,已知船在静水中的航速为vc,那么,(1)怎样渡河时间最短?(2)若vs<vc怎样渡河位移最小?(3)若vs>vc,怎样渡河船漂下的距离最短?
[例9]一条宽度为L的河,水流速度为vs,已知船在静水中的航速为vc,那么,(1)怎样渡河时间最短?(2)若vs<vc怎样渡河位移最小?(3)若vs>vc,怎样渡河船漂下的距离最短?
分析与解:(1)如图2甲所示,设船上头斜向上游与河岸成任意角θ,这时船速在垂直于河岸方向的速度分量V1=Vcsinθ,渡河所需时间为: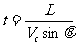 .
.
可以看出:L、Vc一定时,t随sinθ增大而减小;当θ=900时,sinθ=1,所以,当船头与河岸垂直时,渡河时间最短,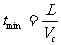 .
.
(2)如图2乙所示,渡河的最小位移即河的宽度。为了使渡河位移等于L,必须使船的合速度V的方向与河岸垂直。这是船头应指向河的上游,并与河岸成一定的角度θ。根据三角函数关系有:Vccosθ─Vs=0.
所以θ=arccosVs/Vc,因为0≤cosθ≤1,所以只有在Vc>Vs时,船才有可能垂直于河岸横渡。
(3)如果水流速度大于船上在静水中的航行速度,则不论船的航向如何,总是被水冲向下游。怎样才能使漂下的距离最短呢?如图2丙所示,设船头Vc与河岸成θ角,合速度V与河岸成α角。可以看出:α角越大,船漂下的距离x越短,那么,在什么条件下α角最大呢?以Vs的矢尖为圆心,以Vc为半径画圆,当V与圆相切时,α角最大,根据cosθ=Vc/Vs,船头与河岸的夹角应为:θ=arccosVc/Vs.
船漂的最短距离为: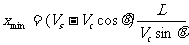 . 此时渡河的最短位移为:
. 此时渡河的最短位移为: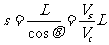 .
.
思考:①小船渡河过程中参与了哪两种运动?这两种运动有何关系?
②过河的最短时间和最短位移分别决定于什么?
1、运动的合成与分解的应用
合运动与分运动的关系:满足等时性与独立性.即各个分运动是独立进行的,不受其他运动的影响,合运动和各个分运动经历的时间相等,讨论某一运动过程的时间,往往可直接分析某一分运动得出.
[例2]小船从甲地顺水到乙地用时t1,返回时逆水行舟用时t2,若水不流动完成往返用时t3,设船速率与水流速率均不变,则( )
A.t3>t1+t2 ; B.t3=t1+t2; C.t3<t1+t2 ; D.条件不足,无法判断
解析:设船的速度为V,水的速度为v0,则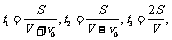
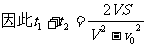
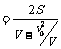 <
<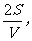 故选C
故选C
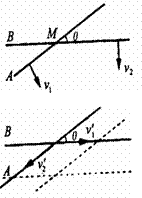
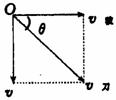
[例3]如图所示,A、B两直杆交角为θ,交点为M,若两杆各以垂直于自身的速度V1、V2沿着纸面运动,则交点M的速度为多大?
解析:如图所示,若B杆不动,A杆以V1速度运动,交点将沿B杆移动,速度为V ,V
,V =V1/sinθ.若A杆不动,B杆移动时,交点M将沿A杆移动,速
=V1/sinθ.若A杆不动,B杆移动时,交点M将沿A杆移动,速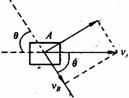 度为V
度为V ,V
,V =V2/sinθ.两杆一起移动时,交点M的速度vM可看成两个分速度V
=V2/sinθ.两杆一起移动时,交点M的速度vM可看成两个分速度V 和V
和V 的合速度,故vM的大小为vM=
的合速度,故vM的大小为vM=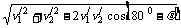 =
=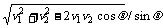
 [例4]玻璃板生产线上,宽9m的成型玻璃板以4
[例4]玻璃板生产线上,宽9m的成型玻璃板以4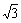 m/s的速度连续不断地向前行进,在切割工序处,金刚钻的走刀速度为8m/s,为了使割下的玻璃板都成规定尺寸的矩形,金刚钻割刀的轨道应如何控制?切割一次的时间多长?
m/s的速度连续不断地向前行进,在切割工序处,金刚钻的走刀速度为8m/s,为了使割下的玻璃板都成规定尺寸的矩形,金刚钻割刀的轨道应如何控制?切割一次的时间多长?
解析:要切成矩形则割刀相对玻璃板的速度垂直v,如图设v刀与v玻方向夹角为θ,cosθ=v玻/v刀=4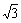 /8,则θ=300。v=
/8,则θ=300。v=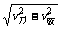 =
=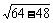 =4m/s。时间t=s/v=9/4=2·45s
=4m/s。时间t=s/v=9/4=2·45s
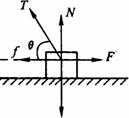
 [例5]如图所示的装置中,物体A、B的质量mA>mB。最初,滑轮两侧的轻绳都处于竖直方向,若用水平力F向右拉A,起动后,使B匀速上升。设水平地面对A的摩擦力为f,绳对A的拉力为T,则力f,T及A所受合力F合的大小()
[例5]如图所示的装置中,物体A、B的质量mA>mB。最初,滑轮两侧的轻绳都处于竖直方向,若用水平力F向右拉A,起动后,使B匀速上升。设水平地面对A的摩擦力为f,绳对A的拉力为T,则力f,T及A所受合力F合的大小()
A.F合≠O,f减小,T增大;B.F合≠O,f增大,T不变;
C. F合=O,f增大,T减小;D. F合=O,f减小,T增大;
 分析:显然此题不能整体分析。B物体匀速上升为平衡状态,所受的绳拉力T恒等于自身的重力,保持不变。A物体水平运动,其速度可分解为沿绳长方向的速度(大小时刻等于B物体的速度)和垂直于绳长的速度(与B物体的速度无关),写出A物体速度与B物体速度的关系式,可以判断是否匀速,从而判断合力是否为零。
分析:显然此题不能整体分析。B物体匀速上升为平衡状态,所受的绳拉力T恒等于自身的重力,保持不变。A物体水平运动,其速度可分解为沿绳长方向的速度(大小时刻等于B物体的速度)和垂直于绳长的速度(与B物体的速度无关),写出A物体速度与B物体速度的关系式,可以判断是否匀速,从而判断合力是否为零。
解:隔离B物体:T=mBg,保持不变。隔离A物体:受力分析如图所示,设绳与水平线夹角为θ,则:
①随A物体右移,θ变小,由竖直平衡可以判断支持力变大。由f=μN,得f变大。
②将A物体水平运动分解如图所示,有vB=vAcosθ,故随θ变小,cosθ变大,VB不变,VA变小,A物体速度时时改变,必有F合≠O。
所得结论为:F合≠O,f变大,T不变。B项正确。
[例6]两个宽度相同但长度不同的台球框固定在水平面上,从两个框的长边同时以相同的速度分别发出小球A和B,如图所示,设球与框边碰撞时无机械能损失,不计摩擦,则两球回到最初出发的框边的先后是( )
A. A球先回到出发框边
B球先回到出发框边
C.两球同时回到出发框边
D.因两框长度不明,故无法确定哪一个球先回到出发框边
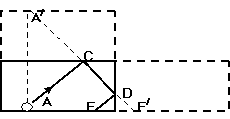 解析:小球与框边碰撞无机械能损失,小球每次碰撞前后的运动速率不变,且遵守反射定律。以A球进行分析,如图。
解析:小球与框边碰撞无机械能损失,小球每次碰撞前后的运动速率不变,且遵守反射定律。以A球进行分析,如图。
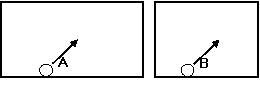 小球沿AC方向运动至C处与长边碰后,沿CD方向运动到D处与短边相碰,最后沿DE回到出发边。经对称得到的直线A/CDE/的长度与折线ACDE的总长度相等。
小球沿AC方向运动至C处与长边碰后,沿CD方向运动到D处与短边相碰,最后沿DE回到出发边。经对称得到的直线A/CDE/的长度与折线ACDE的总长度相等。
框的长边不同,只要出发点的速度与方向相同,不论D点在何处,球所通过的总路程总是相同的,不计碰撞时间,故两球应同时到达最初出发的框边。答案:C
也可用分运动的观点求解:小球垂直于框边的分速度相同,反弹后其大小也不变,回到出发边运动的路程为台球桌宽度的两倍,故应同时回到出发边。
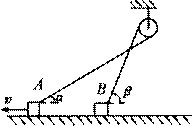
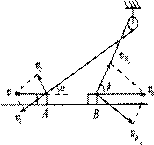 [例7]如图所示,A、B两物体系在跨过光滑定滑轮的一根轻绳的两端,当A物体以速度v向左运动时,系A,B的绳分别与水平方向成a、β角,此时B物体的速度大小为
,方向
[例7]如图所示,A、B两物体系在跨过光滑定滑轮的一根轻绳的两端,当A物体以速度v向左运动时,系A,B的绳分别与水平方向成a、β角,此时B物体的速度大小为
,方向
解析:根据A,B两物体的运动情况,将两物体此时的速度v和vB分别分解为两个分速度v1(沿绳的分量)和v2(垂直绳的分量)以及vB1(沿绳的分量)和vB2(垂直绳的分量),如图,由于两物体沿绳的速度分量相等,v1=vB1,vcosα=vBcosβ.
则B物体的速度方向水平向右,其大小为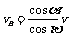
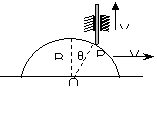 [例8]一个半径为R的半圆柱体沿水平方向向右以速度V0匀速运动。在半圆柱体上搁置一根竖直杆,此杆只能沿竖直方向运动,如图7所示。当杆与半圆柱体接触点P与柱心的连线与竖直方向的夹角为θ,求竖直杆运动的速度。
[例8]一个半径为R的半圆柱体沿水平方向向右以速度V0匀速运动。在半圆柱体上搁置一根竖直杆,此杆只能沿竖直方向运动,如图7所示。当杆与半圆柱体接触点P与柱心的连线与竖直方向的夹角为θ,求竖直杆运动的速度。
解析:设竖直杆运动的速度为V1,方向竖直向上,由于弹力方向沿OP方向,所以V0、V1在OP方向的投影相等,即有 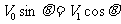 ,解得V1=V0.tgθ.
,解得V1=V0.tgθ.
3.重点掌握的两种情况:一是加速度大小、方向都不变的曲线运动,叫匀变曲线运动,如平抛运动;另一是加速度大小不变、方向时刻改变的曲线运动,如匀速圆周运动.
规律方法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com