
3.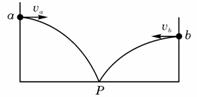 如图,在同一竖直面内,小球a、b从高度不同的两点,分别以初速度va和vb沿水平方向抛出,经过时间ta和tb后落到与两出点水平距离相等的P点。若不计空气阻力,下列关系式正确的是
如图,在同一竖直面内,小球a、b从高度不同的两点,分别以初速度va和vb沿水平方向抛出,经过时间ta和tb后落到与两出点水平距离相等的P点。若不计空气阻力,下列关系式正确的是
A
A. ta>tb, va<vb B. ta>tb, va>vb
C. ta<tb, va<vb D. ta>tb, va>vb
2.关于做平抛运动的物体,正确的说法是
A.速度始终不变 B.加速度始终不变
C.受力始终与运动方向垂直 D.受力始终与运动方向平行
答案:B
[解析]平抛运动是曲线运动,方向时刻在改变,选项A、C、D错误。受力特点是只有重力,加速度为重力加速度,选项B正确。
1.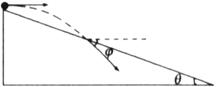 如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上。物体与斜面接触时速度与水平方向的夹角φ满足
如图所示,一物体自倾角为θ的固定斜面顶端沿水平方向抛出后落在斜面上。物体与斜面接触时速度与水平方向的夹角φ满足
A.tanφ=sinθ B. tanφ=cosθ
C. tanφ=tanθ D. tanφ=2tanθ
答案:D
解析:竖直速度与水平速度之比为:tanφ = ,竖直位移与水平位移之比为:tanθ = ,故tanφ =2 tanθ ,D正确。
3、平抛运动的拓展(类平抛运动)
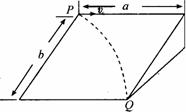 [例7]如图所示,光滑斜面长为a,宽为b,倾角为θ,一物块沿斜面左上方顶点P水平射入,而从右下方顶点Q离开斜面,求入射初速度.
[例7]如图所示,光滑斜面长为a,宽为b,倾角为θ,一物块沿斜面左上方顶点P水平射入,而从右下方顶点Q离开斜面,求入射初速度.
解析:物块在垂直于斜面方向没有运动,物块沿斜面方向上的曲线运动可分解为水平方向上初速度v0的匀速直线运动和沿斜面向下初速度为零的匀加速运动.
在沿斜面方向上mgsinθ=ma加 a加=gsinθ………①,
水平方向上的位移s=a=v0t……②,
沿斜面向下的位移y=b=½ a加t2……③,
由①②③得v0=a·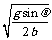
说明:运用运动分解的方法来解决曲线运动问题,就是分析好两个分运动,根据分运动的运动性质,选择合适的运动学公式求解
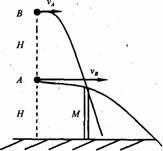 [例8]从高H处的A点水平抛出一个物体,其水平射程为2s。若在A点正上方高H的B点抛出另一个物体,其水平射程为s。已知两物体的运动轨迹在同一竖直平面内,且都从同一竖屏M的顶端擦过,如图所示,求屏M的高度h?
[例8]从高H处的A点水平抛出一个物体,其水平射程为2s。若在A点正上方高H的B点抛出另一个物体,其水平射程为s。已知两物体的运动轨迹在同一竖直平面内,且都从同一竖屏M的顶端擦过,如图所示,求屏M的高度h?
分析:思路1:平抛运动水平位移与两个因素有关:初速大小和抛出高度,分别写出水平位移公式,相比可得初速之比,设出屏M的顶端到各抛出点的高度,分别写出与之相应的竖直位移公式,将各自时间用水平位移和初速表示,解方程即可。
思路2:两点水平抛出,轨迹均为抛物线,将“都从同一竖屏M的顶端擦过”转化为数学条件:两条抛物线均过同一点。按解析几何方法求解。
解析:画出各自轨迹示意图
法一:由平抛运动规律根据题意得
2s=VAtA……①,s=VBtB……②,H=½gtA2……③, 2H=½gtB2……④
可得: ,又设各自经过时间t1、t2从屏M的顶端擦过,则在竖直方向上有H-h=½gt12,2H-h=½gt22,在水平方向上有x=vAt1=vBt2,由以上三式解得h=6H/7。
,又设各自经过时间t1、t2从屏M的顶端擦过,则在竖直方向上有H-h=½gt12,2H-h=½gt22,在水平方向上有x=vAt1=vBt2,由以上三式解得h=6H/7。
法二:由平抛运动规律可得抛物线方程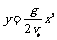 ,依题意有yA=H-h,yB=2H-h时所对应的x值相同,将(x,yA)(x,yB)分别代入各自的抛物线方程联立求出h=6H/7。
,依题意有yA=H-h,yB=2H-h时所对应的x值相同,将(x,yA)(x,yB)分别代入各自的抛物线方程联立求出h=6H/7。
[例9]排球场总长18m,网高2.25 m,如图所示,设对方飞来一球,刚好在3m线正上方被我方运动员后排强攻击回。假设排球被击回的初速度方向是水平的,那么可认为排球被击回时做平抛运动。(g取10m/s2)
(1)若击球的高度h=2.5m,球击回的水平速度与底线垂直,球既不能触网又不出底线,则球被击回的水平速度在什么范围内?
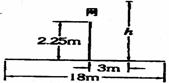 (2)若运动员仍从3m线处起跳,起跳高度h满足一定条件时,会出现无论球的水平初速多大都是触网或越界,试求h满足的条件。
(2)若运动员仍从3m线处起跳,起跳高度h满足一定条件时,会出现无论球的水平初速多大都是触网或越界,试求h满足的条件。
[解析](1)球以vl速度被击回,球正好落在底线上,则t1=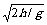 ,vl=s/t1
,vl=s/t1
将s=12m,h=2.5m代入得v1=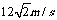 ;
;
球以v2速度被击回,球正好触网,t2=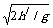 ,v2=s//t2
,v2=s//t2
将h/=(2.5-2.25)m=0.25m,s/=3m代入得v2=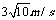 。故球被击目的速度范围是
。故球被击目的速度范围是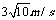 <v≤
<v≤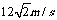 。
。
(2)若h较小,如果击球速度大,会出界,如果击球速度小则会融网,临界情况是球刚好从球网上过去,落地时又刚好压底线,则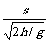 =
=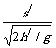 ,s、s/的数值同(1)中的值,h/=
h-2.25(m),由此得 h=2.4m
,s、s/的数值同(1)中的值,h/=
h-2.25(m),由此得 h=2.4m
故若h<2.4m,无论击球的速度多大,球总是触网或出界。
试题展示
2、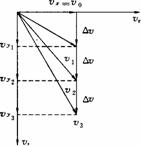 平抛运动的速度变化和重要推论
平抛运动的速度变化和重要推论
①水平方向分速度保持vx=v0.竖直方向,加速度恒为g,速度vy =gt,从抛出点起,每隔Δt时间的速度的矢量关系如图所示.这一矢量关系有两个特点:(1)任意时刻的速度水平分量均等于初速度v0; (2)任意相等时间间隔Δt内的速度改变量均竖直向下,且Δv=Δvy=gΔt.
 ②平抛物体任意时刻瞬时时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。
②平抛物体任意时刻瞬时时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。
证明:设时间t内物体的水平位移为s,竖直位移为h,则末速度的水平分量vx=v0=s/t,而竖直分量vy=2h/t,
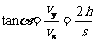 , 所以有
, 所以有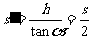
[例5]作平抛运动的物体,在落地前的最后1s内,其速度方向由跟竖直方向成600角变为跟竖直方向成450角,求:物体抛出时的速度和高度分别是多少?
解析一:设平抛运动的初速度为v0,运动时间为t,则经过(t一1)s时vy=g(t一1),
tan300=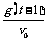
经过ts时:vy=gt,tan450=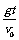 ,∴
,∴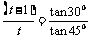 ,
,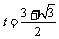
V0=gt/tan450=23.2 m/s.H=½gt2=27. 5 m.
解析二:此题如果用结论解题更简单.
ΔV=gΔt=9. 8m/s.又有V0cot450一v0cot600=ΔV,解得V0=23. 2 m/s,
H=vy2/2g=27. 5 m.
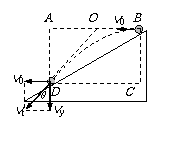 说明:此题如果画出最后1s初、末速度的矢量图,做起来更直观.
说明:此题如果画出最后1s初、末速度的矢量图,做起来更直观.
[例6] 从倾角为θ=30°的斜面顶端以初动能E=6J向下坡方向平抛出一个小球,则小球落到斜面上时的动能E /为______J。
解:以抛出点和落地点连线为对角线画出矩形ABCD,可以证明末速度vt的反向延长线必然交AB于其中点O,由图中可知AD∶AO=2∶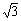 ,由相似形可知vt∶v0=
,由相似形可知vt∶v0=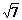 ∶
∶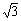 ,因此很容易可以得出结论:E /=14J。
,因此很容易可以得出结论:E /=14J。
1、平抛运动的分析方法
用运动合成和分解方法研究平抛运动,要根据运动的独立性理解平抛运动的两分运动,即水平方向的匀速直线运动和竖直方向的自由落体运动.其运动规律有两部分:一部分是速度规律,一部分是位移规律.对具体的平抛运动,关键是分析出问题中是与位移规律有关还是与速度规律有关
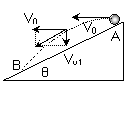 [例2]如图在倾角为θ的斜面顶端A处以速度V0水平抛出一小球,落在斜面上的某一点B处,设空气阻力不计,求(1)小球从A运动到B处所需的时间;(2)从抛出开始计时,经过多长时间小球离斜面的距离达到最大?
[例2]如图在倾角为θ的斜面顶端A处以速度V0水平抛出一小球,落在斜面上的某一点B处,设空气阻力不计,求(1)小球从A运动到B处所需的时间;(2)从抛出开始计时,经过多长时间小球离斜面的距离达到最大?
解析:(1)小球做平抛运动,同时受到斜面体的限制,设从小球从A运动到B处所需的时间为t,则:水平位移为x=V0t
竖直位移为y=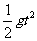 , 由数学关系得到:
, 由数学关系得到: 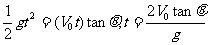
(2)从抛出开始计时,经过t1时间小球离斜面的距离达到最大,当小球的速度与斜面平行时,小球离斜面的距离达到最大。因Vy1=gt1=V0tanθ,所以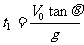
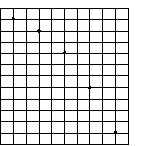 [例3] 已知方格边长a和闪光照相的频闪间隔T,求:v0、g、vc
[例3] 已知方格边长a和闪光照相的频闪间隔T,求:v0、g、vc
解:水平方向: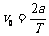 竖直方向:
竖直方向: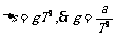
先求C点的水平分速度vx和竖直分速度vy,再求合速度vC:
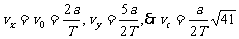
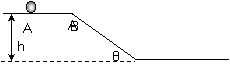 [例4]如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以V0=5m/s的速度在平面上向右运动。求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2)。某同学对此题的解法为:小球沿斜面运动,则
[例4]如图所示,一高度为h=0.2m的水平面在A点处与一倾角为θ=30°的斜面连接,一小球以V0=5m/s的速度在平面上向右运动。求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2)。某同学对此题的解法为:小球沿斜面运动,则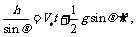 由此可求得落地的时间t。问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果。
由此可求得落地的时间t。问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果。
解析:不同意。小球应在A点离开平面做平抛运动,而不是沿斜面下滑。
正确做法为:落地点与A点的水平距离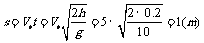
斜面底宽 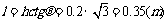
因为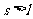 ,所以小球离开A点后不会落到斜面,因此落地时间即为平抛运动时间。
,所以小球离开A点后不会落到斜面,因此落地时间即为平抛运动时间。
∴ 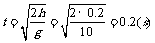
2、处理平抛物体的运动时应注意:
① 水平方向和竖直方向的两个分运动是相互独立的,其中每个分运动都不会因另一个分运动的存在而受到影响--即垂直不相干关系;
② 水平方向和竖直方向的两个分运动具有等时性,运动时间由高度决定,与v0无关;
③ 末速度和水平方向的夹角不等于位移和水平方向的夹角,由上证明可知tgβ=2tgα
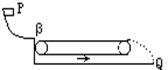 [例1] 物块从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带以后落到地面上的Q点,若传送带的皮带轮沿逆时针方向转动起来,使传送带随之运动,如图所示,再把物块放到P点自由滑下则
[例1] 物块从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带以后落到地面上的Q点,若传送带的皮带轮沿逆时针方向转动起来,使传送带随之运动,如图所示,再把物块放到P点自由滑下则
A.物块将仍落在Q点
B.物块将会落在Q点的左边
C.物块将会落在Q点的右边
D.物块有可能落不到地面上
解答:物块从斜面滑下来,当传送带静止时,在水平方向受到与运动方向相反的摩擦力,物块将做匀减速运动。离开传送带时做平抛运动。当传送带逆时针转动时物体相对传送带都是向前运动,受到滑动摩擦力方向与运动方向相反。 物体做匀减速运动,离开传送带时,也做平抛运动,且与传送带不动时的抛出速度相同,故落在Q点,所以A选项正确。
[小结]若此题中传送带顺时针转动,物块相对传送带的运动情况就应讨论了。
(1)当v0=vB物块滑到底的速度等于传送带速度,没有摩擦力作用,物块做匀速运动,离开传送带做平抛的初速度比传送带不动时的大,水平位移也大,所以落在Q点的右边。
(2)当v0>vB物块滑到底速度小于传送带的速度,有两种情况,一是物块始终做匀加速运动,二是物块先做加速运动,当物块速度等于传送带的速度时,物体做匀速运动。这两种情况落点都在Q点右边。
(3)v0<vB当物块滑上传送带的速度大于传送带的速度,有两种情况,一是物块一直减速,二是先减速后匀速。第一种落在Q点,第二种落在Q点的右边。
规律方法
1、平抛运动:将物体沿水平方向抛出,其运动为平抛运动.
(1)运动特点:a、只受重力;b、初速度与重力垂直.尽管其速度大小和方向时刻在改变,但其运动的加速度却恒为重力加速度g,因而平抛运动是一个匀变速曲线运动
 (2)平抛运动的处理方法:平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动。水平方向和竖直方向的两个分运动既具有独立性,又具有等时性.
(2)平抛运动的处理方法:平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动。水平方向和竖直方向的两个分运动既具有独立性,又具有等时性.
(3)平抛运动的规律:以物体的出发点为原点,沿水平和竖直方向建成立坐标。
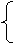
 ax=0……①
ay=0……④
ax=0……①
ay=0……④
水平方向 vx=v0 ……② 竖直方向 vy=gt……⑤
x=v0t……③ y=½gt2……⑥
①平抛物体在时间t内的位移S可由③⑤两式推得s=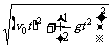 =
=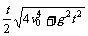 ,
,
②位移的方向与水平方向的夹角α由下式决定tgα=y/x=½gt2/v0t=gt/2v0
③平抛物体经时间t时的瞬时速度vt可由②⑤两式推得vt=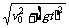 ,
,
④速度vt的方向与水平方向的夹角β可由下式决定tgβ=vy/vx=gt/v0
⑤平抛物体的轨迹方程可由③⑥两式通过消去时间t而推得:y=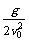 ·x2,
可见,平抛物体运动的轨迹是一条抛物线.
·x2,
可见,平抛物体运动的轨迹是一条抛物线.
⑥运动时间由高度决定,与v0无关,所以t=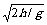 ,水平距离x=v0t=v0
,水平距离x=v0t=v0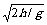
⑦Δt时间内速度改变量相等,即△v=gΔt,ΔV方向是竖直向下的.说明平抛运动是匀变速曲线运动.
9.质量为m的飞机以水平速度V0飞离跑道后逐渐上升,若飞机在此过程中水平速度保持不变,同时受到重力和竖直向上的恒定升力(该升力由其他力的合力提供,不含重力).今测得当飞机在水平方向的位移为L时,它的上升高度为h.求:飞机受到的升力大小;
解:飞机水平方向速度不变,则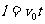 ,竖直方向上飞机加速度恒定,则有
,竖直方向上飞机加速度恒定,则有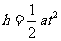 ,
,
解得 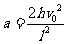 .
.
据牛顿第二定律,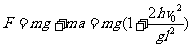
第二单元 平抛物体的运动
基础知识
8.小船在200 m宽的河中横渡,水流速度为2 m/s,船在静水中的航速是4 m/s,求:
(1)当小船的船头始终正对对岸时,它将在何时、何地到达对岸?
⑵要使小船到达正对岸,应如何行驶?历时多长?
解:(1)小船垂直河岸渡河所用时间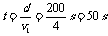
所以小船沿水流方向运动的位移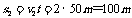
(2)设小船要到正对岸,船头应与河岸成θ角,斜向上游.则有
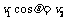 ,∴
,∴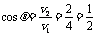 ,
,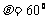
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com