3.特点：简谐运动的图象是正弦(或余弦)曲线．

2.坐标系：以横轴表示时间，纵轴表示位移，用平滑曲线连接各时刻对应的位移末端即得

1.物理意义：表示振动物体(或质点)的位移随时间变化的规律．

说明:简谐运动的位移、回复力、加速度、速度都随时间做周期性变化(正弦或余弦函数)，变化周期为T，振子的动能、势能也做周期性变化，周期为 T／2。

①凡离开平衡位置的过程，v、E_k均减小，x、F、a、E_P均增大；凡向平衡位置移动时，v、E_k均增大, x、F、a、E_P均减小.

②振子运动至平衡位置时，x、F、a为零，E_P最小，v、E_k最大；当在最大位移时，x、F、a、E_P最大，v、E_k最为零；

③在平衡位置两侧的对称点上,x、F、a、v、E_k、E_P的大小均相同．

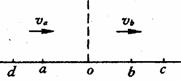[例3]如图所示，一弹簧振子在振动过程中，经a、b两点的速度相同，若它从a到b历时0．2s，从b再回到a的最短时间为0．4s，则该振子的振动频率为(　　 )。

　　 (A)1Hz；(B)1.25Hz　 (C)2Hz；(D) 2．5Hz

　 解析：振子经a、b两点速度相同，根据弹簧振子的运动特点，不难判断a、b两点对平衡位置(O点)一定是对称的，振子由b经O到a所用的时间也是0．2s，由于“从b再回到a的最短时间是0．4s，”说明振子运动到b后是第一次回到a点，且Ob不是振子的最大位移。设图中的c、d为最大位移处，则振子从b→c→b历时0．2s，同理，振子从a→d→a，也历时0．2s，故该振子的周期T＝0．8s，根据周期和频率互为倒数的关系，不难确定该振子的振动频率为1．25Hz。　　 综上所述，本题应选择(B)。

4、在水平方向上振动的弹簧振子的回复力是弹簧的弹力；在竖直方向上振动的弹簧振子的回复力是弹簧弹力和重力的合力。

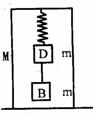[例2]如图所示，在质量为M的无下底的木箱顶部用一轻弹簧悬挂质量均为m(M≥m)的D、B两物体．箱子放在水平地面上，平衡后剪断D、B间的连线，此后D将做简谐运动．当D运动到最高点时，木箱对地压力为(　　　　 )

　　 A、Mg； B．(M－m)g； C、(M+m)g ；　 D、(M+2m)g

[解析]当剪断D、B间的连线后，物体D与弹簧一起可当作弹簧振子，它们将作简谐运动，其平衡位置就是当弹力与D的重力相平衡时的位置．初始运动时D的速度为零，故剪断D、B连线瞬间D相对以后的平衡位置的距离就是它的振幅，弹簧在没有剪断D、B连线时的伸长量为x₁＝2 mg／k，在振动过程中的平衡位置时的伸长量为x₂＝mg／k，故振子振动过程中的振幅为　 A＝x₂－x₁= mg／k

D物在运动过程中，能上升到的最大高度是离其平衡位移为A的高度，由于D振动过程中的平衡位置在弹簧自由长度以下mg／k处，刚好弹簧的自由长度处就是物D运动的最高点，说明了当D运动到最高点时，D对弹簧无作用力，故木箱对地的压力为木箱的重力Mg．

点评：一般说来，弹簧振子在振动过程中的振幅的求法均是先找出其平衡位置，然后找出当振子速度为零时的位置，这两个位置间的距离就是振幅．本题侧重在弹簧振子运动的对称性．解答本题还可以通过求D物运动过程中的最大加速度，它在最高点具有向下的最大加速度，说明了这个系统有部分失重，从而确定木箱对地面的压力

3、可以证明，竖直放置的弹簧振子的振动也是简谐运动，周期公式也是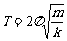。这个结论可以直接使用。

2、弹簧振子振动周期：T=2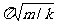，只由振子质量和弹簧的劲度决定，与振幅无关，也与弹簧振动情况(如水平方向振动或竖直方向振动或在光滑的斜面上振动或在地球上或在月球上或在绕地球运转的人造卫星上)无关。

1、一个可作为质点的小球与一根弹性很好且不计质量的弹簧相连组成一个弹簧振子．一般来讲，弹簧振子的回复力是弹力(水平的弹簧振子)或弹力和重力的合力(竖直的弹簧振子)提供的．弹簧振子与质点一样，是一个理想的物理模型．

2、简谐振动：物体所受的回复力跟位移大小成正比时，物体的振动是简偕振动．

①受力特征：回复力F=-KX。

②运动特征：加速度a=一kx／m，方向与位移方向相反，总指向平衡位置。简谐运动是一种变加速运动，在平衡位置时，速度最大，加速度为零；在最大位移处，速度为零，加速度最大。

说明：①判断一个振动是否为简谐运动的依据是看该振动中是否满足上述受力特征或运动特征。

②简谐运动中涉及的位移、速率、加速度的参考点，都是平衡位置.

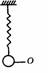
[例1]如图，轻质弹簧上端固定，下端连结一小球，平衡时小球处于O位置，现将小球由O位置再下拉一小段距离后释放(在弹性限度内)，试证明释放后小球的上下振动是简谐振动，

证明：设小球的质量为m，弹簧的劲度系数为k，小球处在O位置有：

mg-kΔx=0………①

式中Δx为小球处在O位置时弹簧的伸长量．

再设小球离开O点的位移x(比如在O点的下方)，并取x为矢量正方向，

此时小球受到的合外力∑F_x为：∑F_x =mg－k(x+Δx)②

由①②两式可得：∑F_x =－kx,　

　　　 所以小球的振动是简谐振动，O点即其振动的平衡位置．

　 点评：这里的F=-kx，不是弹簧的弹力，而是弹力与重力的合力，即振动物体的回复力．此时弹力为k(x+Δx)；所以求回复力时F＝kx，x是相对平衡位置的位移，而不是相对弹簧原长的位移．

1、振动描述的物理量

(1)位移：由平衡位置指向振动质点所在位置的有向线段．　　

①是矢量，其最大值等于振幅；

②始点是平衡位置，所以跟回复力方向永远相反；

③位移随时间的变化图线就是振动图象．

(2)振幅：离开平衡位置的最大距离．

①是标量；　　　 ②表示振动的强弱；

(3)周期和频率：完成一次全变化所用的时间为周期T，每秒钟完成全变化的次数为频率f．

①二者都表示振动的快慢；

②二者互为倒数；T=1/f；

③当T和f由振动系统本身的性质决定时(非受迫振动)，则叫固有频率与固有周期是定值，固有周期和固有频率与物体所处的状态无关．