
2.波的时间的周期性
在x轴上同一个给定的质点,在t+nT时刻的振动情况与它在t时刻的振动情况(位移、速度、加速度等)相同.因此,在t时刻的波形,在t+nT时刻会多次重复出现.这就是机械波的时间的周期性.
波的时间的周期性,表明波在传播过程中,经过整数倍周期时,其波的图象相同.
波动图象的多解涉及:(1)波的空间的周期性;(2)波的时间的周期性;(3)波的双向性;(4)介质中两质点间距离与波长关系未定;(5)介质中质点的振动方向未定.
1.波的空间的周期性
沿波的传播方向,在x轴上任取一点P(x),如图所示,P点的振动完全重复波源O的振动,只是时间上比O点要落后Δt,且Δt =x/v=xT0/λ.在同一波线上,凡坐标与P点坐标x之差为波长整数倍的许多质点,在同一时刻t的位移都与坐标为λ的质点的振动位移相同,其振动速度、加速度也与之相同,或者说它们的振动“相貌”完全相同.因此,在同一波线上,某一振动“相貌”势必会不断重复出现,这就是机械波的空间的周期性.
空间周期性说明,相距为波长整数倍的多个质点振动情况完全相同.
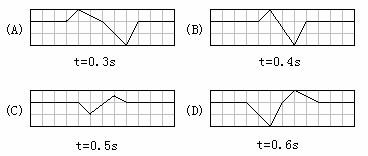
8、两个不等幅的脉冲波在均匀介质中均以 1.0m/s的速率沿同一直线相向传播,t = 0时刻的波形如图所示,图中小方格的边长为 0.1m。则以下不同时刻,波形正确的是 (ABD)

专题:振动图像与波的图像及多解问题
7、声波属于机械波。下列有关声波的描述中正确的是 ( C)
A.同一列声波在各种介质中的波长是相同的
B.声波的频率越高,它在空气中传播的速度越快
C.声波可以绕过障碍物传播,即它可以发生衍射
D.人能辨别不同乐器同时发出的声音,证明声波不会发生干涉
6、一列在竖直方向振动的简谐横波,波长为 ,沿正方向传播,某一时刻,在振动位移向上且大小等于振幅一半的各点中,任取相邻的两点P1、P2,已知P1的x坐标小于P2的x坐标。
,沿正方向传播,某一时刻,在振动位移向上且大小等于振幅一半的各点中,任取相邻的两点P1、P2,已知P1的x坐标小于P2的x坐标。
A. 若P1P2< ,则P1向下运动,P2向上运动
,则P1向下运动,P2向上运动
B. 若P1P2< ,则P1向上运动,P2向下运动
,则P1向上运动,P2向下运动
C. 若P1P2> ,则P1向上运动,P2向下运动
,则P1向上运动,P2向下运动
D. 若P1P2> ,则P1向下运动,P2向上运动
,则P1向下运动,P2向上运动
[答案]:A、C
5、如图所示,位于介质I和II分界面上的波源S,产生两列分别沿x轴负方向与正方向传播的机械波。若在两种介质中波的频率及传播速度分别为f1、f2和v1、v2,则C
 A.f1=2f2,v1=v2
A.f1=2f2,v1=v2
B.f1=f2,v1=0.5v2
C.f1=f2,v1=2v2
D.f1=0.5f2,v1=v2
4、.有两列简谐横波a、b在同一媒质中沿x轴正方向传播,波速均为v=2.5m/s。在t=0时,两列波的波峰正好在x=2.5m处重合,如图所示。
(1)求两列波的周期Ta和Tb。
(2)求t=0时,两列波的波峰重合处的所有位置。
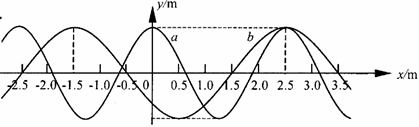 (3)辨析题:分析并判断在t=0时是否存在两列波的波谷重合处。
(3)辨析题:分析并判断在t=0时是否存在两列波的波谷重合处。
某同学分析如下:既然两列波的波峰存在重合处,那么波谷与波谷重合处也一定存在。只要找到这两列波半波长的最小公倍数,……,即可得到波谷与波谷重合处的所有位置。
你认为该同学的分析正确吗?若正确,求出这些点的位置。若不正确,指出错误处并通过计算说明理由。
解析:
(1)从图中可以看出两列波的波长分别为λa=2.5m,λb=4.0m,因此它们的周期分别为
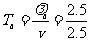 s=1s
s=1s  s=1.6s
s=1.6s
(2)两列波的最小公倍数为 S=20m
t=0时,两列波的波峰生命处的所有位置为
x=(2.5 20k)m,k=0,1,2,3,……
20k)m,k=0,1,2,3,……
(3)该同学的分析不正确。
要找两列波的波谷与波谷重合处,必须从波峰重合处出发,找到这两列波半波长的厅数倍恰好相等的位置。设距离x=2.5m为L处两列波的波谷与波谷相遇,并设
L=(2m-1) L=(2n-1),式中m、n均为正整数
L=(2n-1),式中m、n均为正整数
只要找到相应的m、n即可
将λa=2.5m,λb=4.0m代入并整理,得
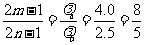
由于上式中m、n在整数范围内无解,所以不存在波谷与波谷重合处。
3、下列关于简谐振动和简谐机械波的说法正确的是 ( )
A.弹簧振子的周期与振幅有关
B.横波在介质中的传播速度由介质本身的性质决定
C.在波传播方向上的某个质点的振动速度就是波的传播速度
D.单位时间内经过媒质中一点的完全波的个数就是这列简谐波的频率
答案: BD
2、 一列简谐横波沿x轴正方向传播,振幅为A。t=0时, 平衡位置在x=0处的质元位于y=0处, 且向y轴负方向运动;此时,平衡位置在x=0.15m处的质元位于y=A处.该波的波长可能等于
A.0.60m B.0.20m C.0.12m D.0.086m
答案:AC
解析:因为波沿正方向传播,且x=0处质点经平衡位置向y轴负方向运动,故此时波形图为正弦函数图像,则x=0.15m= ,当n=0时,
,当n=0时, ,A项正确;当n=1时,
,A项正确;当n=1时,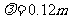 ,C项正确;当n
,C项正确;当n 3时,
3时, ,D项错。
,D项错。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com