
23. In general, Osama Bin Laden is ______ to move frequently among his Qaida terrorist camps and deep caves in Afghanistan(阿富汗).
A. known B. found C. hoped D. believed
22. ---I haven’t seen your daughter for a long time. How is she? I guess she must be a big girl now.
---Yeah, she___. Like any other teenager, she is completely___ my control. She seldom takes my advice.
A. surely is ,over B. is surely, out of C. is sure, under D. sure is, beyond
第一节 单项填空(共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白出的最佳答案。
21. -What would you like to order, maybe ________coffee?
-No, thank you! What is __________special today?
A. a; the B. the; a C. the; the D. /; /
7. (本小题满分14分)
 第21题 |
设双曲线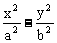 =1( a > 0, b > 0 )的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点.
=1( a > 0, b > 0 )的右顶点为A,P是双曲线上异于顶点的一个动点,从A引双曲线的两条渐近线的平行线与直线OP分别交于Q和R两点.
(1) 证明:无论P点在什么位置,总有|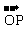 |2 = |
|2 = | ·
·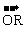 | ( O为坐标原点);
| ( O为坐标原点);
(2) 若以OP为边长的正方形面积等于双曲线实、虚轴围成的矩形面积,求双曲线离心率的取值范围;
解:(1) 设OP:y
= k x, 又条件可设AR:
y =  (x – a ),
(x – a ),
解得: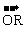 = (
= (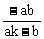 ,
, ), 同理可得
), 同理可得 = (
= (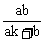 ,
,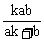 ),
),
∴| ·
· | =|
| =|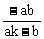
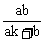 +
+
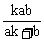 | =
| = .
4分
.
4分
设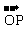 = ( m, n ) , 则由双曲线方程与OP方程联立解得:
= ( m, n ) , 则由双曲线方程与OP方程联立解得:
m2 =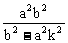 , n2 =
, n2 =  ,
,
∴ |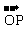 |2 = :m2 + n2 =
|2 = :m2 + n2 = 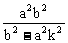 +
+  =
= ,
,
∵点P在双曲线上,∴b2 – a2k2 > 0 .
∴无论P点在什么位置,总有|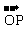 |2 = |
|2 = | ·
· | .
4分
| .
4分
(2)由条件得: = 4ab, 2分
= 4ab, 2分
即k2 =  > 0 , ∴
4b > a, 得e >
> 0 , ∴
4b > a, 得e >  2分
2分
6.(14分)已知数列 中,
中, ,当
,当 时,其前
时,其前 项和
项和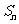 满足
满足 ,
,
(2)
求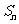 的表达式及
的表达式及 的值;
的值;
(3)
求数列 的通项公式;
的通项公式;
(4)
设 ,求证:当
,求证:当 且
且 时,
时,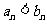 .
.
解:(1)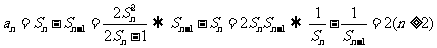
所以 是等差数列.则
是等差数列.则 .
.
 .
.
(2)当 时,
时, ,
,
综上, .
.
(3)令 ,当
,当 时,有
时,有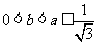 (1)
(1)
法1:等价于求证 .
.
当 时,
时, 令
令
 ,
,
则 在
在 递增.
递增.
又 ,
,
所以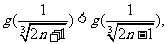 即
即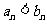 .
.
法(2)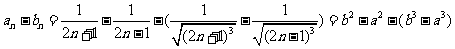
 (2)
(2)

 (3)
(3)
因 ,所以
,所以
由(1)(3)(4)知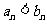 .
.
法3:令 ,则
,则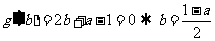
所以
因 则
则 ,
,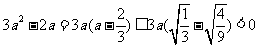
所以 (5)
(5)
由(1)(2)(5)知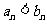
5.(12分) 、
、 是椭圆
是椭圆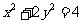 的左、右焦点,
的左、右焦点, 是椭圆的右准线,点
是椭圆的右准线,点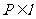 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 、
、 两点.
两点.
(1)
 当
当 时,求
时,求 的面积;
的面积;
(2)
当 时,求
时,求 的大小;
的大小;
(3)
求 的最大值.
的最大值.
解:(1)
(2)因 ,
,
则
(1)
设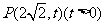

 ,
,
当 时,
时,
4.(本小题满分14分)已知函数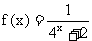
 .
.
(1) 试证函数 的图象关于点
的图象关于点 对称;
对称;
(2) 若数列 的通项公式为
的通项公式为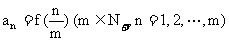 , 求数列
, 求数列 的前m项和
的前m项和
(3) 设数列 满足:
满足:  ,
,  . 设
. 设 .
.
若(2)中的 满足对任意不小于2的正整数n,
满足对任意不小于2的正整数n,  恒成立, 试求m的最大值.
恒成立, 试求m的最大值.
解: (1)设点 是函数
是函数 的图象上任意一点, 其关于点
的图象上任意一点, 其关于点 的对称点为
的对称点为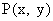 .
.
由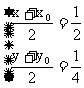 得
得
所以, 点P的坐标为P .………………(2分)
.………………(2分)
由点 在函数
在函数 的图象上, 得
的图象上, 得 .
.
∵

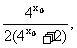 ∴点P
∴点P 在函数
在函数 的图象上.
的图象上.
∴函数 的图象关于点
的图象关于点 对称. ………………(4分)
对称. ………………(4分)
(2)由(1)可知,
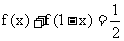 , 所以
, 所以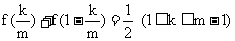 ,
,
即 ………………(6分)
………………(6分)
由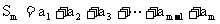 , ………………
①
, ………………
①
得 ………………②
………………②
由①+②, 得
∴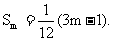 ………………(8分)
………………(8分)
(3) ∵
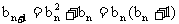 , ………………③
, ………………③
∴对任意的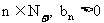 . ………………④
. ………………④
由③、④, 得 即
即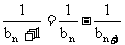 .
.
∴ .……………(10分)
.……………(10分)
∵ ∴数列
∴数列 是单调递增数列.
是单调递增数列.
∴ 关于n递增. 当
关于n递增. 当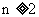 , 且
, 且 时,
时,  .
.
∵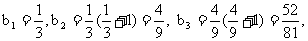
∴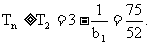 ………………(12分)
………………(12分)
∴ 即
即 ∴
∴ ∴m的最大值为6. ……………(14分)
∴m的最大值为6. ……………(14分)
3.(本小题满分12分)将圆O:  上各点的纵坐标变为原来的一半 (横坐标不变),
上各点的纵坐标变为原来的一半 (横坐标不变),
得到曲线C.
(1) 求C的方程;
(2) 设O为坐标原点, 过点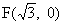 的直线l与C交于A、B两点, N为线段AB的中点,
的直线l与C交于A、B两点, N为线段AB的中点,
延长线段ON交C于点E.
求证:  的充要条件是
的充要条件是 .
.
解: (1)设点 , 点M的坐标为
, 点M的坐标为 ,由题意可知
,由题意可知 ………………(2分)
………………(2分)
又 ∴
∴ .
.
所以, 点M的轨迹C的方程为 .………………(4分)
.………………(4分)
(2)设点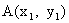 ,
,  , 点N的坐标为
, 点N的坐标为 ,
,
 ㈠当直线l与x轴重合时, 线段AB的中点N就是原点O,
㈠当直线l与x轴重合时, 线段AB的中点N就是原点O,
不合题意,舍去; ………………(5分)
㈡设直线l: 
由 消去x,
消去x,
得 ………………①
………………①
∴ ………………(6分)
………………(6分)
∴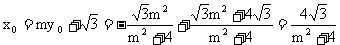 ,
,
∴点N的坐标为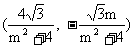 .………………(8分)
.………………(8分)
①若
 , 坐标为, 则点E的为
, 坐标为, 则点E的为 , 由点E在曲线C上,
, 由点E在曲线C上,
得 , 即
, 即 ∴
∴ 舍去).
舍去).
由方程①得
又
∴ .………………(10分)
.………………(10分)
②若 , 由①得
, 由①得 ∴
∴
∴点N的坐标为 , 射线ON方程为:
, 射线ON方程为:
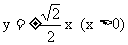 ,
,
由 解得
解得 ∴点E的坐标为
∴点E的坐标为
∴
 .
.
综上, 
 的充要条件是
的充要条件是 .………………(12分)
.………………(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com