1．(17分)如图为一滑梯的示意图，滑梯的长度AB为 L= 5.0m，倾角θ＝37°。 BC段为与滑梯平滑连接的水平地面。一个小孩从滑梯顶端由静止开始滑下，离开B点后在地面上滑行了s = 2.25m后停下。小孩与滑梯间的动摩擦因数为μ = 0.3。不计空气阻力。取g = 10m/s²。已知sin37°= 0.6，cos37°= 0.8。求：

(1)小孩沿滑梯下滑时的加速度a的大小；

(2)小孩滑到滑梯底端B时的速度v的大小；

(3)小孩与地面间的动摩擦因数μ′。

22．(本小题满分14分)

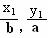设A(x₁，y₁)，B(x₂，y₂)是椭圆=1(a>b>0)上的两点，已知向量m() ,n(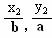),若m·n=0且椭圆的离心率e=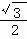，短轴长为2，O为坐标原点：

(Ⅰ)求椭圆的方程：

(Ⅱ)若直线AB过椭圆的焦点F(0,c)，(为半焦距)，求直线AB的斜k率的值：

(Ⅲ)试问：△AOB的面积是否为定值？如果是，请给予证明：如果不是，请说明理由。

山东省利津一中2009-2010学年第一学期模块质量监测

21．(本小题满分12分)

某工厂每天生产某种产品最多不超过40件，并且在生产过程中产品的正品率P与每日生产产品件数(x∈N^※)间的关系为P=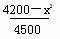，每生产一件正品赢利4000元，每出现一件次品亏损2000元。(注：正品率产品的正品件数÷产品总件数×100%)

(Ⅰ)将日利润y(元)表示成日产量x(件)的函数：

(Ⅱ)求该厂的日产量为多少件时，日利润最大？并求出日利润的最大值。

20．(本小题满分12分)

已知数列{a_n}的各项均是正数，其前n项和为s_n，满足(p-1)S_n=p²-a_n，其中p为正常数，且p≠1。

(Ⅰ)求数列{a_n}的通项公式：

(Ⅱ)设b_n=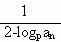(n∈N^※)，数列{b_nb_n+2}的前n项和为T_n，求证：

T_n<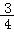

19、(本小题满分12分)

　　 直棱柱ABCD-A₁B₁C₁D₁中，底面ABCD是直角梯形。∠ABD=∠ADC=90°，AB=2AD=2CD=2．

　　 (Ⅰ)求证：AC⊥平面BB₁C₁C；

(Ⅱ)在A₁B₁上是否存在一点p，使得DP与平面DCB₁与平面都平行？证明你的结论。

18、(本小题满分12分)

已知f(x)=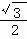sin2x-cos²x-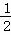，(x∈R)

(1)求函数f(x)的最小值和最小正周期

(2)设△ABC的内角 A、B、C 的对边分别为a、b、c，且c=，f(c)=0若向量m=(1、sinA)与向量n=(2、sinB)共线，求a、b的值。

17．(本小题满分12分) 　　，

　　 现有7名数理化成绩优秀者，其中A₁ 、A₂ 、A₃数学成绩优秀，B₁、B₂物理成绩优秀，C₁、C₂化学成绩优秀．从中选出数学、物理、化学成绩优秀者各1名，组成一个小组代表学校参加竟赛．

　　 (1)求C₁被选中的概率；

(2)求A₁ 和B₁不全被选中的概率。

16．若x²+y²≤m²(m>0},则实数m的取值范围是＿＿＿＿＿＿＿＿＿＿＿＿＿。＿。

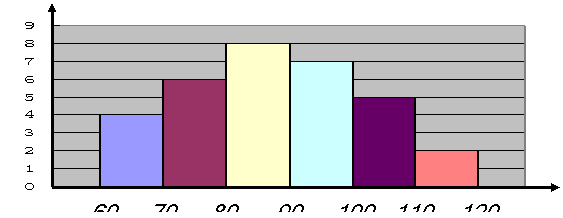
15．　 某中学部分学生参加市高中数学竞赛取得了优异成绩，指导老师统计了所有参赛同学的成绩(成绩都为整数，满分120分)，并且绘制了“频数分布直方图”(如图)，如果90分以上(含90分)获奖，那么该校参赛学生的获奖率为＿＿＿＿＿＿＿。

14、已知等差数列{a_n}的公差d≠0，它的1、5、17项顺次成等比数列，则这个等数列的公比是＿＿＿＿＿＿＿。