
3、共点的三个力的合力大小范围是:合力的最大值为三个力的大小之和。用三个力中最大的一个力的值减去其余两个力,其结果为正,则这个正值为三个力的合力的最小值;若结果为零或负,则三个力的合力的最小值为零。
2、合力可以大于分力,也可以等于分力,或者小于分力。
1、共点的两个力的合力的大小范围是│F1-F2│≤F合≤F1+F2。合力随两力夹角θ的减小而增大。
2、不要把受力分析与力的分解相混淆,受力分析的对象是某一个物体,分析的力是实际受到的性质力;而力的分解的对象则是某一个力,是用分力代替这个力。
合力和分力是一种等效替代关系,求几个已知分力的合力必须要明确这个合力是虚设的等效力,并非真实存在的力,合力没有性质可言,也找不到施力物体。反之,把一个已知力分解为两个分力,这两个分力也并非存在。无性质可言,当然也找不到施力物体。因此在进行受力分析时,要注意以下两点:
1、合力和分力不能同时共存,不能既考虑了合力,又考虑分力,这们就增加了力。
力的分解是力的合成的逆运算,同样遵守平行四边形法则,
㈠关于力分解的讨论:
(1).己知合力的大小和方向,-----有无数多组解(即可分解为无数对分力)
(2).己知合力的大小和方向,
①.又知F1、F2的方向-------有确定的解
②.又知F1、F2大小---------有确定的解
③.又知F1的大小和方向----有确定的解
④.又知F1的方向及F2的大小:当F>F2>Fsin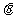 时-----有两组解
时-----有两组解
当F2=Fsin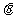 时-----有一组解
时-----有一组解
当F2>F时-----有确定的解
㈡在实际问题中,分力的求解方法:
①根据力产生的实际效果确定分力的方向.即使是同一个力,在不同的情况下所产生的效果也往往是不同的,按问题的需要进行分解
②.由平行四边形定则作出力的分解图
③.由数学知识进行运算,力学 形和几何
形和几何 形相似
形相似
㈢力分解的解题思路:
力分解问题的关键是:根据力的作用效果确定分力的方向.
然后画出力的平行四边形,接着转化为一个根据己知边角关系求角的几何问题.
基本思路可以表示为:
实际问题 确定分力的方向
确定分力的方向 物理抽象作出平行四边形
物理抽象作出平行四边形  用数学计算求分力
用数学计算求分力
 重难点突破
重难点突破
2、 运算法则:
运算法则:
(1)平行四边形法则:
求两个互成角度的共点力F1、F2的合力,可以把F1,F2的线段作为邻边作平行四边形,它的对角线即表示合力的大小和方向。
(2)三角形法则:合力和两个分力通过平移,构成一个首尾相接的封闭三角形。这就是三角形法则
求两个互成角度的共点力F1,F2的合力,可以把F1,F2首尾相接地画出来,把F1,F2的另外两端连接起来,则此连线就表示合力F的大小和方向;
(3)共点的两个力:F1、F2的合力F的大小,与它们的夹角θ有关,θ越大,合力越小;θ越小,合力越大。
合力可能比分力大,也可能比分力小。F1与F2同向时合力最大,F1与F2反向时合力最小。
合力大小的取值范围是 | F1-F2|≤F合≤(F1+F2)
求F 、F2两个共点力的合力的公式:
、F2两个共点力的合力的公式:
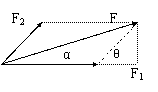
 F=
F=
合力的方向与F1成a角:
tga=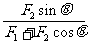


注意:①力的合成和分解都均遵从平行四边行法则。
②两个力的合力范围: ú F1-F2 ú £ F£ F1 +F2
③合力大小可以大于分力、也可以小于分力、也可以等于分力。
④当F1、F2大小一定, 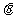 在0-1800范围内变化时,
在0-1800范围内变化时, 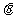 增大, F减小;
增大, F减小;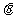 减小, F增大。
减小, F增大。
⑤F1、F2垂直 (正交)
时: F的大小
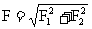 F的方向 tan
F的方向 tan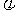 =
=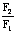
⑥当F1、F2大小相等,夹角为1200时,合力为F=F1=F2 方向与两分力匀为600
(4)三个力或三个以上的力的合力范围在一定的条件下可以是:0≤F≤| F1+F2+…Fn|
1、求几个已知力的合力叫力的合成;求一个力的分力叫力的分解.
(分解某个力时,要根据这个力产生的实际效果进行分解)。
同一个力可以分解成无数对大小、方向不同的分力。下面是有确定解的几种常见情况:
(1)已知合力和两个分力的方向,求两个分力的大小(有一组解)。
(2)已知合力和一个分力的大小与方向,求另一个分力的大小和方向(有一组解)。
(3)已知合力及一个分力F1的大小和F2的方向求F1的方向和F2的大小(有一组解或两组解)。
合力和分力是一种等效代替关系,分解是用分力代换合力;合成则是用合力代换分力
注意:力的合成是唯一的,而力的分解有时不是唯一的。只有在下列两种情形下,力的分解才是唯一的:
(1)已知合力和两个分力的方向; (2)已知合力和一个分力大小和方向。
3、共点力:几个力如果作用在物体的同一个点,或者它们的作用线相交于同一个点,这几个力做共点力。
2、合力与它的分力是力的效果上的一种等效替代关系。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com