11．已知直线l过原点，抛物线C的顶点在原点，焦点在x轴正半轴上，若点A(-1，0)和B(0，8)关于l的对称点都在C上，求直线l和抛物线的方程。

10．设曲线C₁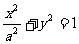：(a为正常数)与C₂：y²=2(x+m)在x轴上方有一个公共点P。(1)求实数m的取值范围(用a表示)；

(2)O为原点，若C₁与x轴的负半轴交于点A，当0<a<时，试求ΔOAP面积的最大值(用a表示)。

9．已知椭圆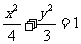的内接ΔABC的边AB，AC分别过左、右焦点F₁，F₂，椭圆的左、右顶点分别为D，E，直线DB与直线CE交于点P，当点A在椭圆上变动时，试求点P的轨迹。

8．已知点P(1，2)既在椭圆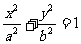内部(含边界)，又在圆x²+y²=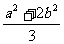外部(含边界)，若a,b∈R⁺,则a+b的最小值为_________.

7．已知抛物线y²=2px及定点A(a,b),B(-a,0),ab≠0,b²≠2pa，M是抛物线上的点，设直线AM，BM与抛物线的另一个交点分别为M₁，M₂，当M变动时，直线M₁M₂恒过一个定点，此定点坐标为_________.

6．长为l(l<1)的线段AB的两端点在抛物线y=x²上滑动，则线段AB的中点M到x轴的最短距离等于_________.

5．ΔABC一边的两顶点坐标为B(0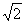，)和C(0，)，另两边斜率的乘积为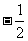，若点T坐标为(t,0)(t∈R⁺),则|AT|的最小值为_________.

4．设F₁，F₂分别是双曲线(a>b>0)的左、右焦点，P为双曲线上的动点，过F₁作∠F₁PF₂平分线的垂线，垂足为M，则M的轨迹为_________.

3．给定椭圆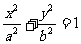，如果存在过左焦点F的直线交椭圆于P，Q两点，且OP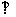OQ，则离心率e的取值范围是_________.

2．设O为抛物线的顶点，F为焦点，且PQ为过F的弦，已知|OF|=a，|PQ|=b，ΔOPQ面积为_________.