
4.直线与平面成角问题。
例8 正方形ABCD中,E,F分别是AB,CD的中点,G为BF的中点,将正方形沿EF折成1200的二面角,求AG和平面EBCF所成的角。
例9 OA是平面α的一条斜角,AB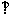 α于B,C在α内,且AC
α于B,C在α内,且AC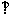 OC,∠AOC=α,∠AOB=β,∠BOC=γ。证明:cosα=cosβ•cosγ.
OC,∠AOC=α,∠AOB=β,∠BOC=γ。证明:cosα=cosβ•cosγ.
3.平行与垂直的论证。
例5 A,B,C,D是空间四点,且四边形ABCD四个角都是直角,求证:四边形ABCD是矩形。
例6 一个四面体有两个底面上的高线相交。证明:它的另两条高线也相交。
例7 在矩形ABCD中,AD=2AB,E是AD中点,沿BE将ΔABE折起,并使AC=AD,求证:平面ABE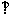 平面BCDE。
平面BCDE。
1.公理的应用。
例1 直线a,b,c都与直线d相交,且a//b,c//b,求证:a,b,c,d共面。
例2 长方体有一个截面是正六边形是它为正方体的什么条件?
2 异面直线的相关问题。
异面直线的相关问题。
例3 正方体的12条棱互为异面直线的有多少对?
例4 正方体,ABCD-A1B1C1D1棱长为1,求面对角线A1C1与AB1所成的角。
公理1 一条直线。上如果有两个不同的点在平面。内.则这条直线在这个平面内,记作:a a.
a.
公理2 两个平面如果有一个公共点,则有且只有一条通过这个点的公共直线,即若P∈α∩β,则存在唯一的直线m,使得α∩β=m,且P∈m。
公理3 过不在同一条直线上的三个点有且只有一个平面。即不共线的三点确定一个平面.
推论l 直线与直线外一点确定一个平面.
推论2 两条相交直线确定一个平面.
推论3 两条平行直线确定一个平面.
公理4 在空间内,平行于同一直线的两条直线平行.
定义1 异面直线及成角:不同在任何一个平面内的两条直线叫做异面直线.过空间任意一点分别作两条异面直线的平行线,这两条直线所成的角中,不超过900的角叫做两条异面直线成角.与两条异面直线都垂直相交的直线叫做异面直线的公垂线,公垂线夹在两条异面直线之间的线段长度叫做两条异面直线之间的距离.
定义2 直线与平面的位置关系有两种;直线在平面内和直线在平面外.直线与平面相交和直线与平面平行(直线与平面没有公共点叫做直线与平面平行)统称直线在平面外.
定义3 直线与平面垂直:如果直线与平面内的每一条直线都垂直,则直线与这个平面垂直.
定理1 如果一条直线与平面内的两条相交直线都垂直,则直线与平面垂直.
定理2 两条直线垂直于同一个平面,则这两条直线平行.
定理3 若两条平行线中的一条与一个平面垂直,则另一条也和这个平面垂直.
定理4 平面外一点到平面的垂线段的长度叫做点到平面的距离,若一条直线与平面平行,则直线上每一点到平面的距离都相等,这个距离叫做直线与平面的距离.
定义5 一条直线与平面相交但不垂直的直线叫做平面的斜线.由斜线上每一点向平面引垂线,垂足叫这个点在平面上的射影.所有这样的射影在一条直线上,这条直线叫做斜线在平面内的射影.斜线与它的射影所成的锐角叫做斜线与平面所成的角.
结论1 斜线与平面成角是斜线与平面内所有直线成角中最小的角.
定理4 (三垂线定理)若d为平面。的一条斜线,b为它在平面a内的射影,c为平面a内的一条直线,若c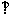 b,则c
b,则c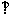 a.逆定理:若c
a.逆定理:若c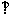 a,则c
a,则c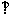 b.
b.
定理5 直线d是平面a外一条直线,若它与平面内一条直线b平行,则它与平面a平行
定理6 若直线。与平面α平行,平面β经过直线a且与平面a交于直线6,则a//b.
结论2 若直线。与平面α和平面β都平行,且平面α与平面β相交于b,则a//b.
定理7 (等角定理)如果一个角的两边和另一个角的两边分别平行且方向相同,则两个角相等.
定义6 平面与平面的位置关系有两种:平行或相交.没有公共点即平行,否则即相交.
定理8 平面a内有两条相交直线a,b都与平面β平行,则α//β.
定理9 平面α与平面β平行,平面γ∩α=a,γ∩β=b,则a//b.
定义7 (二面角),经过同一条直线m的两个半平面α,β(包括直线m,称为二面角的棱)所组成的图形叫二面角,记作α-m-β,也可记为A-m一B,α-AB-β等.过棱上任意一点P在两个半平面内分别作棱的垂线AP,BP,则∠APB(≤900)叫做二面角的平面角.
它的取值范围是[0,π].
特别地,若∠APB=900,则称为直二面角,此时平面与平面的位置关系称为垂直,即α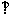 β.
β.
定理10 如果一个平面经过另一个平面的垂线,则这两个平面垂直.
定理11 如果两个平面垂直,过第一个平面内的一点作另一个平面的垂线在第一个平面内.
定理12 如果两个平面垂直,过第一个子面内的一点作交线的垂线与另一个平面垂直.
定义8 有两个面互相平行而其余的面都是平行四边形,并且每相邻两个平行四边形的公共边(称为侧棱)都互相平行,由这些面所围成的几何体叫做棱柱.两个互相平行的面叫做底面.如果底面是平行四边形则叫做平行六面体;侧棱与底面垂直的棱柱叫直棱柱;底面是正多边形的直棱柱叫做正棱柱.底面是矩形的直棱柱叫做长方体.棱长都相等的正四棱柱叫正方体.
定义9 有一个面是多边形(这个面称为底面),其余各面是一个有公共顶点的三角形的多面体叫棱锥.底面是正多边形,顶点在底面的射影是底面的中心的棱锥叫正棱锥.
定理13 (凸多面体的欧拉定理)设多面体的顶点数为V,棱数为E,面数为F,则
V+F-E=2.
定义10 空间中到一个定点的距离等于定长的点的轨迹是一个球面.球面所围成的几何体叫做球.定长叫做球的半径,定点叫做球心.
定理14 如果球心到平面的距离d小于半径R,那么平面与球相交所得的截面是圆面,圆心与球心的连线与截面垂直.设截面半径为r,则d2+r2=R2.过球心的截面圆周叫做球大圆.经过球面两点的球大圆夹在两点间劣弧的长度叫两点间球面距离.
定义11 (经度和纬度)用平行于赤道平面的平面去截地球所得到的截面四周叫做纬线.纬线上任意一点与球心的连线与赤道平面所成的角叫做这点的纬度.用经过南极和北极的平面去截地球所得到的截面半圆周(以两极为端点)叫做经线,经线所在的平面与本初子午线所在的半平面所成的二面角叫做经度,根据位置不同又分东经和西经.
定理15 (祖 原理)夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.
定理16 (三面角定理)从空间一点出发的不在同一个平面内的三条射线共组成三个角.其中任意两个角之和大于另一个,三个角之和小于3600.
定理17 (面积公式)若一个球的半径为R,则它的表面积为S球面=4πR2。若一个圆锥的母线长为l,底面半径为r,则它的侧面积S侧=πrl.
定理18 (体积公式)半径为R的球的体积为V球=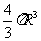 ;若棱柱(或圆柱)的底面积为s,高h,则它的体积为V=sh;若棱锥(或圆锥)的底面积为s,高为h,则它的体积为V=
;若棱柱(或圆柱)的底面积为s,高h,则它的体积为V=sh;若棱锥(或圆锥)的底面积为s,高为h,则它的体积为V=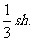
定理19 四面体ABCD中,记∠BDC=α,∠ADC=β,∠ADB=γ,∠BAC=A,∠ABC=B,∠ACB=C。DH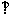 平面ABC于H。
平面ABC于H。
(1)射影定理:SΔABD•cosФ=SΔABH,其中二面角D-AB-H为Ф。
(2)正弦定理: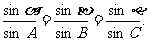
(3)余弦定理:cosα=cosβcosγ+sinβsinγcosA.
cosA=-cosBcosC+sinBsinCcosα.
(4)四面体的体积公式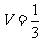 DH•SΔABC
DH•SΔABC
=
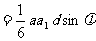 (其中d是a1, a之间的距离,
(其中d是a1, a之间的距离,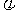 是它们的夹角)
是它们的夹角)
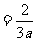 SΔABD•SΔACD•sinθ(其中θ为二面角B-AD-C的平面角)。
SΔABD•SΔACD•sinθ(其中θ为二面角B-AD-C的平面角)。
6.已知BC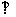 CD,点A为BD中点,点Q在BC上,AC=CQ,又在BQ上找一点R,使BR=2RQ,CQ上找一点S,使QS=RQ,求证:∠ASB=2∠DRC。
CD,点A为BD中点,点Q在BC上,AC=CQ,又在BQ上找一点R,使BR=2RQ,CQ上找一点S,使QS=RQ,求证:∠ASB=2∠DRC。
5.直角ΔABC斜边为AB,内切圆切BC,CA,AB分别于D,E,F点,AD交内切圆于P点。若CP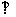 BP,求证:PD=AE+AP。
BP,求证:PD=AE+AP。
4.在坐标平面内,从原点出发以同一初速度v0和不同发射角(即发射方向与x轴正向之间 的夹角)α(α∈[0,π],α≠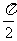 )射出的质点,在重力的作用下运动轨迹是抛物线,所有这些抛物线组成一个抛物线族,若两条抛物线在同一个交点处的切线互相垂直,则称这个交点为正交点。证明:此抛物线族的所有正交点的集合是一段椭圆弧,并求此椭圆弧的方程(确定变量取值范围)。
)射出的质点,在重力的作用下运动轨迹是抛物线,所有这些抛物线组成一个抛物线族,若两条抛物线在同一个交点处的切线互相垂直,则称这个交点为正交点。证明:此抛物线族的所有正交点的集合是一段椭圆弧,并求此椭圆弧的方程(确定变量取值范围)。
3.以B0和B1为焦点的椭圆与ΔAB0B1的边ABi交于Ci(i=0,1),在AB0的延长线上任取点P0,以B0为圆心,B0P0为半径作圆弧 交C1B0的延长线于Q0;以C1为圆心,C1Q0为半径作圆弧Q0P1交B1A的延长线于P1;B1为圆心,B1P1为半径作圆弧P1Q1交B1C0的延长线于Q1;以C0为圆心,C0Q1为半径作圆弧Q1
交C1B0的延长线于Q0;以C1为圆心,C1Q0为半径作圆弧Q0P1交B1A的延长线于P1;B1为圆心,B1P1为半径作圆弧P1Q1交B1C0的延长线于Q1;以C0为圆心,C0Q1为半径作圆弧Q1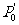 ,交AB0的延长线于
,交AB0的延长线于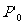 。求证:(1)点
。求证:(1)点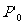 与点P0重合,且圆弧P0Q0与P0Q1相内切于P0;(2)P0,Q0,P1,Q1共圆。
与点P0重合,且圆弧P0Q0与P0Q1相内切于P0;(2)P0,Q0,P1,Q1共圆。
2.求证:在坐标平面上不存在一条具有奇数个顶点,每段长都为1的闭折线,它的每个顶点坐标都是有理数。
1.在四边形ABCD中,对角线AC平分∠BAD,在CD上取一点E,BE与AC相交于F,延长DF交BC于G,求证:∠GAC=∠EAC。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com