5．若a,b为两条异面直线，过空间一点O与a,b都平行的平面有__________个。

4．正方体ABCD-A₁B₁C₁D₁中，E，F分别是面ADD₁A₁、面ABCD的中心，G为棱CC₁中点，直线C₁E，GF与AB所成的角分别是α，β。则α+β=__________。

3．动点P从棱长为a的正方体的一个顶点出发，沿棱运动，每条棱至多经过一次，则点P运动的最大距离为__________。

2．空间中有四个点E，F，G，H，命题甲：E，F，G，H不共面；命题乙：直线EF和GH不相交，则甲是乙的__________条件。

1．正三角形ABC的边长为4，到A，B，C的距离都是1的平面有__________个.

9．四面体中的问题。

例16　 已知三棱锥S-ABC的底面是正三角形，A点在侧面SBC上的射影H是ΔSBC的垂心，二面角H-AB-C的平面角等于30⁰，SA=。求三棱锥S-ABC的体积。

例17　 设d是任意四面体的相对棱间距离的最小值，h是四面体的最小高的长，求证：2d>h.

注：在前面例题中除用到教材中的公理、定理外，还用到了向量法、体积法、射影法，请读者在解题中认真总结。

8．与球有关的问题。

例15　 圆柱直径为4R，高为22R，问圆柱内最多能装半径为R的球多少个？

7．凸多面体的欧拉公式。

例14　 一个凸多面体有32个面，每个面或是三角形或是五边形，对于V个顶点每个顶点均有T个三角形面和P个五边形面相交，求100P+10T+V。

6．距离问题。

例12　 正方体ABCD-A₁B₁C₁D₁的棱长为a，求对角线AC与BC₁的距离。

例13在三棱维S-ABC中，底面是边长为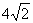的正三角形，棱SC的长为2，且垂直于底面，E，D分别是BC，AB的中点，求CD与SE间的距离。

[分析]　 取BD中点F，则EF//CD，从而CD//平面SEF，要求CD与SE间的距离就转化为求点C到平面SEF间的距离。

5．二面角问题。

例10设S为平面ABC外一点，∠ASB=45⁰，∠CSB=60⁰，二面角A-SB-C为直角二面角，求∠ASC的余弦值。

例11　 已知直角ΔABC的两条直角边AC=2，BC=3，P为斜边AB上一点，沿CP将此三角形折成直二面角A-CP-B，当AB=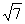时，求二面角P-AC-B的大小。