
9.顶点为P的圆锥的轴截面是等腰直角三角形,A是底面圆围上的点,B是底面圆内的点,O为底面圆圆心,AB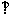 OB,垂足为B,OH
OB,垂足为B,OH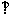 PB,垂足为H,且PA=4,C为PA的中点,则当三棱锥C-HPC体积最大时,OB=_________。
PB,垂足为H,且PA=4,C为PA的中点,则当三棱锥C-HPC体积最大时,OB=_________。
8.由曲线x2=4y,x2=-4y,x=4,x=-4围成的图形绕y轴旋转一周所得旋转体的体积为V1,满足x2+y2≤16,x2+(y-2)2≥4,x2+(y+2)2≥4的点(x,y)组成的图形绕y轴旋转一周所得旋转体的体积为V2,则 _________。
_________。
7.一个球与正四面体的六条棱都相切,正四面体棱长为a,这个球的体积为_________。
6.空间三条直线a,b,c两两成异面直线,那么与a,b,c都相交的直线有_________条。
5.将给定的两个全等的正三棱锥的底面粘在一起,恰得到一个所有二面角都相等的六面体,并且该六面体的最短棱长为2,则最远两个顶点间距离为_________。
4.棱锥M-ABCD的底面是正方形,且MA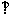 AB,如果ΔAMD的面积为1,则能放入这个棱锥的最大球的半径为_________.
AB,如果ΔAMD的面积为1,则能放入这个棱锥的最大球的半径为_________.
3.已知三个平面α,β,γ每两个平面之间的夹角都是 ,且
,且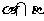 =a,
=a,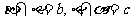 ,命题甲:
,命题甲: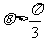 ;命题乙:a,b,c相交于一点。则甲是乙的_________条件。
;命题乙:a,b,c相交于一点。则甲是乙的_________条件。
2.一个六面体的各个面和一个正八面体的各个面都是边长为a的正三角形,这两个多面体的内切球的半径之比是一个既约分数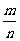 ,那么mn=_________。
,那么mn=_________。
1.现有边长分别为3,4,5的三角形两个,边长分别为4,5,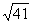 的三角形四个,边长分别为
的三角形四个,边长分别为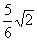 ,4,5的三角形六个,用上述三角形为面,可以拼成_________个四面体。
,4,5的三角形六个,用上述三角形为面,可以拼成_________个四面体。
13.三棱锥S-ABC中,侧棱SA,SB,SC两两互相垂直,M为ΔABC的重心,D为AB中点,作与SC平行的直线DP,证明:(1)DP与SM相交;(2)设DP与SM的交点为 ,则
,则 为三棱锥S-ABC外接球球心。
为三棱锥S-ABC外接球球心。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com