6．设平面α，β，γ，δ与四面体ABCD的外接球面分别切于点A，B，C，D。证明：如果平面α与β的交线与直线CD共面，则γ与δ的交线与直线AB共面。

5．四面体ABCD的四条高AA₁，BB₁，CC₁，DD₁相交于H点(A₁，B₁，C₁，D₁分别为垂足)。三条高上的内点A₂，B₂，C₂满足AA₂：AA=BB₂：B₂B₁=CC₂：C₂C₁=2：1。证明：H，A₂，B₂，C₂，D₁在同一个球面上。

4．空间是否存在有限点集M，使得对M中的任意两点A，B，可以在M中另取两点C，D，使直线AB和CD互相平行但不重合。

3．P，A，B，C，D是空间五个不同的点，∠APB=∠BPC=∠CPD=∠DPA=θ，这里θ为已知锐角，试确定∠APC+∠BPD的最大值和最小值。

2．P，Q是正四面体A-BCD内任意两点，求证：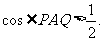

1．能否在棱长为1的正方体形状的盒子里放入三个彼此至多有一个公共点的棱长为1的正四面体？

13．过正四面体ABCD的高AH作一平面，与四面体的三个侧面交于三条直线，这三条直线与四面体的底面夹角为α，β，γ，求tan²α+tan²β+tan²γ之值。

12．在四面体ABCD中，∠BDC=90⁰，D到平面ABC的垂线的垂足S是ΔABC的垂心，试证：(AB+BC+CA)²≤6(AD²+BD²+CD²)，并说明等号成立时是一个什么四面体？

11．设空间被分为5个不交的非空集合，证明：一定有一个平面，它至少与其中的四个集合有公共点。

10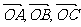．是三个互相垂直的单位向量，π是过点O的一个平面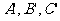，分别是A，B，C在π上的射影，对任意的平面π，由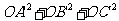构成的集合为_________。