

11.互斥事件:不可能同时发生的两个事件,叫做互斥事件,也叫不相容事件。如果事件A1,A2,…,An彼此互斥,那么A1,A2,…,An中至少有一个发生的概率为
p(A1+A2+…+An)= p(A1)+p(A2)+…+p(An).
10.等可能事件的概率,如果一次试验中共有n种等可能出现的结果,其中事件A包含的结果有m种,那么事件A的概率为p(A)=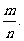
9.随机事件:在一定条件下可能发生也可能不发生的事件叫随机事件。在大量重复进行同一试验时,事件A发生的频率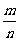 总是接近于某个常数,在它附近摆动,这个常数叫做事件A发生的概率,记作p(A),0≤p(A)≤1.
总是接近于某个常数,在它附近摆动,这个常数叫做事件A发生的概率,记作p(A),0≤p(A)≤1.
8.二项式定理:若n∈N+,则(a+b)n=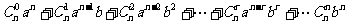 .其中第r+1项Tr+1=
.其中第r+1项Tr+1=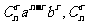 叫二项式系数。
叫二项式系数。
7.定理1:不定方程x1+x2+…+xn=r的正整数解的个数为 。
。
[证明]将r个相同的小球装入n个不同的盒子的装法构成的集合为A,不定方程x1+x2+…+xn=r的正整数解构成的集合为B,A的每个装法对应B的唯一一个解,因而构成映射,不同的装法对应的解也不同,因此为单射。反之B中每一个解(x1,x2,…,xn),将xi作为第i个盒子中球的个数,i=1,2,…,n,便得到A的一个装法,因此为满射,所以是一一映射,将r个小球从左到右排成一列,每种装法相当于从r-1个空格中选n-1个,将球分n份,共有 种。故定理得证。
种。故定理得证。
推论1 不定方程x1+x2+…+xn=r的非负整数解的个数为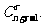
推论2 从n个不同元素中任取m个允许元素重复出现的组合叫做n个不同元素的m可重组合,其组合数为
6.组合数的基本性质:(1)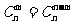 ;(2)
;(2)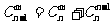 ;(3)
;(3) ;(4)
;(4)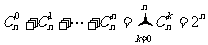 ;(5)
;(5)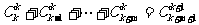 ;(6)
;(6)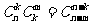 。
。
5.组合与组合数:一般地,从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合,即从n个不同元素中不计顺序地取出m个构成原集合的一个子集。从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数,用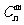 表示:
表示:
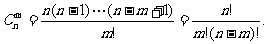
4.N个不同元素的圆周排列数为 =(n-1)!。
=(n-1)!。
3.排列与排列数:从n个不同元素中,任取m(m≤n)个元素,按照一定顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列,从n个不同元素中取出m个(m≤n)元素的所有排列个数,叫做从n个不同元素中取出m个元素的排列数,用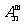 表示,
表示,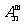 =n(n-1)…(n-m+1)=
=n(n-1)…(n-m+1)=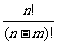 ,其中m,n∈N,m≤n,
,其中m,n∈N,m≤n,
注:一般地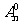 =1,0!=1,
=1,0!=1,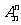 =n!。
=n!。
1.加法原理:做一件事有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,那么完成这件事一共有N=m1+m2+…+mn种不同的方法。
2 乘法原理:做一件事,完成它需要分n个步骤,第1步有m1种不同的方法,第2步有m2种不同的方法,……,第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×…×mn种不同的方法。
乘法原理:做一件事,完成它需要分n个步骤,第1步有m1种不同的方法,第2步有m2种不同的方法,……,第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×…×mn种不同的方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com