
2.加法原理。
例2 没有电流通过电流表,其原因仅因为电阻断路的可能性共有几种?
1.乘法原理。
例1 有2n个人参加收发电报培训,每两个人结为一对互发互收,有多少种不同的结对方式?
19.几何分布:在独立重复试验中,某事件第一次发生时所做试验的次数ξ也是一个随机变量,若在一次试验中该事件发生的概率为p,则p(ξ=k)=qk-1p(k=1,2,…),ξ的分布服从几何分布,Eξ=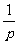 ,Dξ=
,Dξ=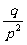 (q=1-p).
(q=1-p).
18.二项分布:如果在一次试验中某事件发生的概率是p,那么在n次独立重复试验中,这个事件恰好发生k次的概率为p(ξ=k)=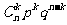 , ξ的分布列为
, ξ的分布列为
|
ξ |
0 |
1 |
… |
xi |
… |
N |
|
p |
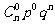 |
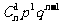 |
… |
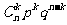 |
… |
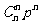 |
此时称ξ服从二项分布,记作ξ-B(n,p).若ξ-B(n,p),则Eξ=np,Dξ=npq,以上q=1-p.
17.离散型随机为量的分布列:如果随机试验的结果可以用一个变量来表示,那么这样的变量叫随机变量,例如一次射击命中的环数ξ就是一个随机变量,ξ可以取的值有0,1,2,…,10。如果随机变量的可能取值可以一一列出,这样的随机变量叫离散型随机变量。
一般地,设离散型随机变量ξ可能取的值为x1,x2,…,xi,…,ξ取每一个值xi(i=1,2,…)的概率p(ξ=xi)=pi,则称表
|
ξ |
x1 |
x2 |
x3 |
… |
xi |
… |
|
p |
p1 |
p2 |
p3 |
… |
pi |
… |
为随机变量ξ的概率分布,简称ξ的分布列,称Eξ=x1p1+x2p2+…+xnpn+…为ξ的数学期望或平均值、均值、简称期望,称Dξ=(x1-Eξ)2•p1+(x2-Eξ)2•p2+…+(xn-Eξ)2pn+…为ξ的均方差,简称方差。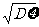 叫随机变量ξ的标准差。
叫随机变量ξ的标准差。
16.独立重复试验的概率:如果在一次试验中,某事件发生的概率为p,那么在n次独立重复试验中,这个事件恰好发生k次的概率为pn(k)=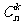 •pk(1-p)n-k.
•pk(1-p)n-k.
15.独立重复试验:若n次重复试验中,每次试验结果的概率都不依赖于其他各次试验的结果,则称这n次试验是独立的.
14.相互独立事件同时发生的概率:两个相互独立事件同时发生的概率,等于每个事件发生的概率的积。即p(A•B)=p(A)•p(B).若事件A1,A2,…,An相互独立,那么这n个事件同时发生的概率为p(A1•A2• … •An)=p(A1)•p(A2)• … •p(An).
13.相互独立事件:事件A(或B)是否发生对事件B(或A)发生的概率没有影响,这样的两个事件叫做相互独立事件。
12.对立事件:事件A,B为互斥事件,且必有一个发生,则A,B叫对立事件,记A的对立事件为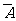 。由定义知p(A)+p(
。由定义知p(A)+p(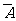 )=1.
)=1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com