12．概率问题的解法。

例14　 如果某批产品中有a件次品和b件正品，采用有放回的抽样方式从中抽取n件产品，问：恰好有k件是次品的概率是多少？

例15　 将一枚硬币掷5次，正面朝上恰好一次的概率不为0，而且与正面朝上恰好两次的概率相同，求恰好三次正面朝上的概率。

例16　 甲、乙两个乒乓球运动员进行乒乓球比赛，已知每一局甲胜的概率为0.6，乙胜的概率为0.4，比赛时可以用三局二胜或五局三胜制，问：在哪一种比赛制度下，甲获胜的可能性大？

例17　 有A，B两个口袋，A袋中有6张卡片，其中1张写有0，2张写有1，3张写有2；B袋中有7张卡片，其中4张写有0，1张写有1，2张写有2。从A袋中取出1张卡片，B袋中取2张卡片，共3张卡片。求：(1)取出3张卡片都写0的概率；(2)取出的3张卡片数字之积是4的概率；(3)取出的3张卡片数字之积的数学期望。

11．二项式定理的应用。

例12　 若n∈N, n≥2，求证：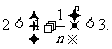

例13　 证明：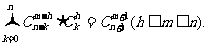

10．组合数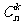的性质。

例10　 证明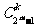：是奇数(k≥1).

例11　 对n≥2,证明：

9．母函数。

例9　 一副三色牌共有32张，红、黄、蓝各10张，编号为1，2，…，10，另有大、小王各一张，编号均为0。从这副牌中任取若干张牌，按如下规则计算分值：每张编号为k的牌计为2^k分，若它们的分值之和为2004，则称这些牌为一个“好牌”组，求好牌组的个数。

8．算两次。

例8　 m,n,r∈N₊，证明：　 ①

7．递推方法。

例7　 用1，2，3三个数字来构造n位数，但不允许有两个紧挨着的1出现在n位数中，问：能构造出多少个这样的n位数？

6．容斥原理。

例6　 由数字1，2，3组成n位数(n≥3)，且在n位数中，1，2，3每一个至少出现1次，问：这样的n位数有多少个？

5．贡献法。

例5　 已知集合A={1，2，3，…，10}，求A的所有非空子集的元素个数之和。

4．映射法。

例4　 如果从1，2，…，14中，按从小到大的顺序取出a₁,a₂,a₃使同时满足：a₂-a₁≥3,a₃-a₂≥3，那么所有符合要求的不同取法有多少种？

3．插空法。

例3　 10个节目中有6个演唱4个舞蹈，要求每两个舞蹈之间至少安排一个演唱，有多少种不同的安排节目演出顺序的方式？