5．一条铁路原有m个车站(含起点，终点)，新增加n个车站(n>1)，客运车票相应地增加了58种，原有车站有_________个。

4．三个人传球，从甲开始发球，每次接球后将球传给另外两人中的任意一个，经5次传球后，球仍回到甲手中的传法有_________种。

3．四面体的顶点和各棱的中点共10个点，在其中任取4个不共面的点，有_________种取法。

2．从{-3,-2,-1,0,1,2,3,4}中任取3个不同元素作为二次函数y=ax²+bx+c的系数，能组成过原点，且顶点在第一或第三象限的抛物线有___________条。

1．若n∈{1,2,…,100}且n是其各位数字和的倍数，则这种n有__________个。

15.一项“过关游戏”规定：在第n关要抛掷一颗骰子n次，如果这n次抛掷所得到的点数之和大于2ⁿ，则算过关。问：(1)某人在这项游戏中最多能过几关？(2)他连过前三关的概率是多少？(注：骰子是一个在各面上分别有1，2，3，4，5，6点数的均匀正方体)

14．已知i,m,n是正整数，且1<i≤m≤n。证明：(1)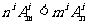；(2)(1+m)ⁿ>(1+n)^m.

13．a,b,c,d,e五个人安排在一个圆桌周围就坐，若a,b不相邻有_________种安排方式。

12．马路上有编号为1，2，3，…，10的十盏路灯，要将其中三盏关掉，但不能同时关掉相邻的两盏或三盏，也不能关掉两端的路灯，则满足条件的关灯方法种数是_________。

11．某人拿着5把钥匙去开门，有2把能打开。他逐个试，试三次之内打开房门的概率是_________。