12．甲、乙两人轮流向同一目标射击，第一次甲射击，以后轮流射击，甲每次击中的概率为p(0<p<1)，乙每次击中的概率为q(0<q<1)，求甲、乙首先击中的概率各是多少？

11．将编号为1，2，…，9这九个小球随机放置在圆周的九个等分点上，每个等分点上各有一个小球，设周围上所有相邻两球的号码之差的绝对值之和为S，求S达到最小值的放法的概率(注：如果某种放法经旋转或镜面反射后可与另一放法重合，则认为是相同的放法)。

10．投掷一次骰子，出现点数1，2，…，6的概率均为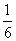，连续掷10次，出现的点数之和是30的概率为_________。

9．求值：=_________。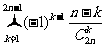

8．如果自然数a各位数字之和等于7，那么称a为“吉祥数”，将所有的吉祥数从小到大排成一列a₁,a₂,a₃,…,若a_n=2005，则a_n=_________。

7．如果a,b,c,d都属于{1,2,3,4}且a≠b,b≠c,c≠d, d≠a；且a是a,b,c,d中的最小值，则不同的四位数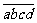的个数为_________。

6．某次乒乓球单打比赛中，原计划每两名选手恰比赛一场，但有3名选手各比赛2场之后就退出了，这样，全部比赛只进行50场，上述三名选手之间比赛场数为_________。

5．骰子的六个面标有1，2，…，6这六个数字，相邻两个面上的数字之差的绝对值叫变差，变差的总和叫全变差V，则全变差V的最大值为_________，最小值为_________。

4．1，2，3，4，5的排列a₁,a₂,a₃,a₄,a₅具有性质：对于1≤i≤4,a₁,a₂,…,a_i不构成1，2，…，i的某个排列，这种排列的个数是_________。

3．已知A={0，1，2，3，4，5，6，7}，映射f:A→A满足：(1)若i≠j，则f(i)≠f(j)；(2)若i+j=7，则f(i)+f(j)=7，这样的映射的个数为_________。