
4.最大值最小值定理:如果f(x)是闭区间[a,b]上的连续函数,那么f(x)在[a,b]上有最大值和最小值。
3.连续:如果函数f(x)在x=x0处有定义,且 f(x)存在,并且
f(x)存在,并且 f(x)=f(x0),则称f(x)在x=x0处连续。
f(x)=f(x0),则称f(x)在x=x0处连续。
1.极限定义:(1)若数列{un}满足,对任意给定的正数ε,总存在正数m,当n>m且n∈N时,恒有|un-A|<ε成立(A为常数),则称A为数列un当n趋向于无穷大时的极限,记为 ,另外
,另外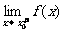 =A表示x大于x0且趋向于x0时f(x)极限为A,称右极限。类似地
=A表示x大于x0且趋向于x0时f(x)极限为A,称右极限。类似地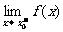 表示x小于x0且趋向于x0时f(x)的左极限。
表示x小于x0且趋向于x0时f(x)的左极限。
2 极限的四则运算:如果
极限的四则运算:如果 f(x)=a,
f(x)=a,  g(x)=b,那么
g(x)=b,那么 [f(x)±g(x)]=a±b,
[f(x)±g(x)]=a±b,  [f(x)•g(x)]=ab,
[f(x)•g(x)]=ab, 
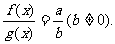
6.证明: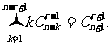

5.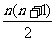 个不同的数随机排成图13-2所示的三角形阵,设Mk是从上往下第k行中的最大数,求M1<M2<…<Mn的概率。
个不同的数随机排成图13-2所示的三角形阵,设Mk是从上往下第k行中的最大数,求M1<M2<…<Mn的概率。
4.设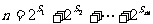 ,其中S1,S2,…,Sm都是正整数且S1<S2<…<Sm,求证组合数
,其中S1,S2,…,Sm都是正整数且S1<S2<…<Sm,求证组合数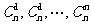 中奇数的个数等于2m。
中奇数的个数等于2m。
3.求从集合{1,2,…,n}中任取满足下列条件的k个数{j1,j2,…,jk}的组合数;(1)1≤j1<j2<…<jk≤n;(2)jh+1-jh≥m,h=1,2,…,k-1,其中m>1为固定的正整数;(3)存在h0,1≤h0≤k-1,使得 ≥m+1.
≥m+1.
2.设S={1,2,…,10},A1,A2,…,Ak是S的k个子集合,满足:(1)|Ai|=5,i=1,2,…,k;(2)|Ai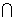 Aj|≤2,1≤i<j≤k,求k的最大值。
Aj|≤2,1≤i<j≤k,求k的最大值。
1.100张卡片上分别写有数字1到100,一位魔术师把这100张卡片放入颜色分别是红色、白色、蓝色的三个盒子里,每个盒子里至少放入一张卡片。
一位观众从三个盒子中挑出两个,并从中各选取一张卡片,然后宣布这两张卡片上的两个数的和数,魔术师知道这个和数之后,便能够指出哪一个是没有被观众取出卡片的盒子。问:共有多少种放卡片的方法,使得这个魔术师总能够成功?(如果至少有一张卡片被放入不同颜色的盒子,两种方法被认为是不同的)
13.设m,n∈N,0<m≤n,求证: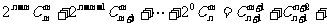 …+
…+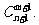
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com