
14.Lagrange中值定理:若f(x)在[a,b]上连续,在(a,b)上可导,则存在ξ∈(a,b),使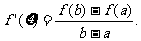
[证明] 令F(x)=f(x)-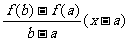 ,则F(x)在[a,b]上连续,在(a,b)上可导,且F(a)=F(b),所以由13知存在ξ∈(a,b)使
,则F(x)在[a,b]上连续,在(a,b)上可导,且F(a)=F(b),所以由13知存在ξ∈(a,b)使 =0,即
=0,即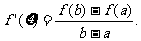
13.罗尔中值定理:若函数f(x)在[a,b]上连续,在(a,b)上可导,且f(a)=f(b),则存在ξ∈(a,b),使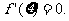
[证明] 若当x∈(a,b),f(x)≡f(a),则对任意x∈(a,b), .若当x∈(a,b)时,f(x)≠f(a),因为f(x)在[a,b]上连续,所以f(x)在[a,b]上有最大值和最小值,必有一个不等于f(a),不妨设最大值m>f(a)且f(c)=m,则c∈(a,b),且f(c)为最大值,故
.若当x∈(a,b)时,f(x)≠f(a),因为f(x)在[a,b]上连续,所以f(x)在[a,b]上有最大值和最小值,必有一个不等于f(a),不妨设最大值m>f(a)且f(c)=m,则c∈(a,b),且f(c)为最大值,故 ,综上得证。
,综上得证。
12.极值的第二充分条件:设f(x)在x0的某领域(x0-δ,x0+δ)内一阶可导,在x=x0处二阶可导,且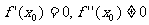 。(1)若
。(1)若 ,则f(x)在x0处取得极小值;(2)若
,则f(x)在x0处取得极小值;(2)若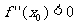 ,则f(x)在x0处取得极大值。
,则f(x)在x0处取得极大值。
11.极值的第一充分条件:设f(x)在x0处连续,在x0邻域(x0-δ,x0+δ)内可导,(1)若当x∈(x-δ,x0)时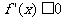 ,当x∈(x0,x0+δ)时
,当x∈(x0,x0+δ)时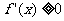 ,则f(x)在x0处取得极小值;(2)若当x∈(x0-δ,x0)时
,则f(x)在x0处取得极小值;(2)若当x∈(x0-δ,x0)时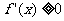 ,当x∈(x0,x0+δ)时
,当x∈(x0,x0+δ)时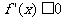 ,则f(x)在x0处取得极大值。
,则f(x)在x0处取得极大值。
10.极值的必要条件:若函数f(x)在x0处可导,且在x0处取得极值,则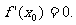
9.导数与函数的性质:(1)若f(x)在区间I上可导,则f(x)在I上连续;(2)若对一切x∈(a,b)有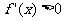 ,则f(x)在(a,b)单调递增;(3)若对一切x∈(a,b)有
,则f(x)在(a,b)单调递增;(3)若对一切x∈(a,b)有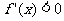 ,则f(x)在(a,b)单调递减。
,则f(x)在(a,b)单调递减。
8.复合函数求导法:设函数y=f(u),u= (x),已知
(x),已知 (x)在x处可导,f(u)在对应的点u(u=
(x)在x处可导,f(u)在对应的点u(u= (x))处可导,则复合函数y=f[
(x))处可导,则复合函数y=f[ (x)]在点x处可导,且(f[
(x)]在点x处可导,且(f[ (x)]
(x)]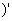 =
= .
.
7.导数的运算法则:若u(x),v(x)在x处可导,且u(x)≠0,则
(1)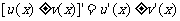 ;(2)
;(2)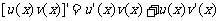 ;(3)
;(3)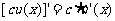 (c为常数);(4)
(c为常数);(4)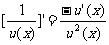 ;(5)
;(5)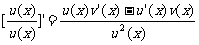 。
。
6.几个常用函数的导数:(1)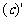 =0(c为常数);(2)
=0(c为常数);(2)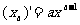 (a为任意常数);(3)
(a为任意常数);(3)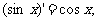 (4)
(4) ;(5)
;(5)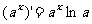 ;(6)
;(6)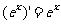 ;(7)
;(7)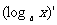
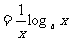 ;(8)
;(8)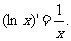
5.导数:若函数f(x)在x0附近有定义,当自变量x在x0处取得一个增量Δx时(Δx充分小),因变量y也随之取得增量Δy(Δy=f(x0+Δx)-f(x0)).若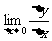 存在,则称f(x)在x0处可导,此极限值称为f(x)在点x0处的导数(或变化率),记作
存在,则称f(x)在x0处可导,此极限值称为f(x)在点x0处的导数(或变化率),记作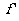 (x0)或
(x0)或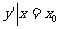 或
或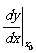 ,即
,即 。由定义知f(x)在点x0连续是f(x)在x0可导的必要条件。若f(x)在区间I上有定义,且在每一点可导,则称它在此敬意上可导。导数的几何意义是:f(x)在点x0处导数
。由定义知f(x)在点x0连续是f(x)在x0可导的必要条件。若f(x)在区间I上有定义,且在每一点可导,则称它在此敬意上可导。导数的几何意义是:f(x)在点x0处导数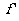 (x0)等于曲线y=f(x)在点P(x0,f(x0))处切线的斜率。
(x0)等于曲线y=f(x)在点P(x0,f(x0))处切线的斜率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com