
1. =_________.
=_________.
7.利用导数讨论极值。
例8 设f(x)=alnx+bx2+x在x1=1和x2=2处都取得极值,试求a与b的值,并指出这时f(x)在x1与x2处是取得极大值还是极小值。
例9 设x∈[0,π],y∈[0,1],试求函数f(x,y)=(2y-1)sinx+(1-y)sin(1-y)x的最小值。
6.利用导数证明不等式。
例7 设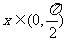 ,求证:sinx+tanx>2x.
,求证:sinx+tanx>2x.
5.用导数讨论函数的单调性。
例6 设a>0,求函数f(x)=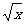 -ln(x+a)(x∈(0,+∞))的单调区间。
-ln(x+a)(x∈(0,+∞))的单调区间。
4.导数的计算。
例5 求下列函数的导数:(1)y=sin(3x+1);(2)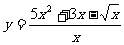 ;(3)y=ecos2x;(4)
;(3)y=ecos2x;(4)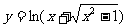 ;(5)y=(1-2x)x(x>0且
;(5)y=(1-2x)x(x>0且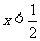 )。
)。
3.利用导数的几何意义求曲线的切线方程。
2.连续性的讨论。
例3 设f(x)在(-∞,+∞)内有定义,且恒满足f(x+1)=2f(x),又当x∈[0,1)时,f(x)=x(1-x)2,试讨论f(x)在x=2处的连续性。
1.极限的求法。
例1 求下列极限:(1)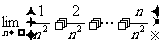 ;(2)
;(2)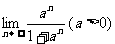 ;(3)
;(3)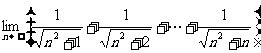 ;(4)
;(4)
例2 求下列极限:(1)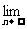 (1+x)(1+x2)(1+
(1+x)(1+x2)(1+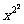 )…(1+
)…(1+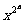 )(|x|<1);
)(|x|<1);
(2) ;(3)
;(3)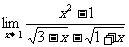 。
。
16.琴生不等式:设α1,α2,…,αn∈R+,α1+α2+…+αn=1。(1)若f(x)是[a,b]上的凸函数,则x1,x2,…,xn∈[a,b]有f(a1x1+a2x2+…+anxn)≤a1f(x1)+a2f(x2)+…+anf(xn).
15.曲线凸性的充分条件:设函数f(x)在开区间I内具有二阶导数,(1)如果对任意x∈I,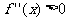 ,则曲线y=f(x)在I内是下凸的;(2)如果对任意x∈I,
,则曲线y=f(x)在I内是下凸的;(2)如果对任意x∈I,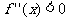 ,则y=f(x)在I内是上凸的。通常称上凸函数为凸函数,下凸函数为凹函数。
,则y=f(x)在I内是上凸的。通常称上凸函数为凸函数,下凸函数为凹函数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com