
12.若a,b,c∈R,a≠0,则关于x的方程ax2+bx+c=0,当Δ=b2-4ac<0时方程的根为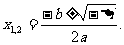
11.实系数方程虚根成对定理:实系数一元n次方程的虚根成对出现,即若z=a+bi(b≠0)是方程的一个根,则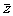 =a-bi也是一个根。
=a-bi也是一个根。
10.代数基本定理:在复数范围内,一元n次方程至少有一个根。
9.复数z是实数的充要条件是z=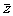 ;z是纯虚数的充要条件是:z+
;z是纯虚数的充要条件是:z+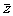 =0(且z≠0).
=0(且z≠0).
8.复数相等的充要条件:(1)两个复数实部和虚部分别对应相等;(2)两个复数的模和辐角主值分别相等。
7.单位根:若wn=1,则称w为1的一个n次单位根,简称单位根,记Z1=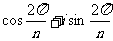 ,则全部单位根可表示为1,
,则全部单位根可表示为1, ,
,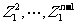 .单位根的基本性质有(这里记
.单位根的基本性质有(这里记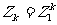 ,k=1,2,…,n-1):(1)对任意整数k,若k=nq+r,q∈Z,0≤r≤n-1,有Znq+r=Zr;(2)对任意整数m,当n≥2时,有
,k=1,2,…,n-1):(1)对任意整数k,若k=nq+r,q∈Z,0≤r≤n-1,有Znq+r=Zr;(2)对任意整数m,当n≥2时,有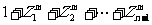 =
=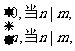 特别1+Z1+Z2+…+Zn-1=0;(3)xn-1+xn-2+…+x+1=(x-Z1)(x-Z2)…(x-Zn-1)=(x-Z1)(x-
特别1+Z1+Z2+…+Zn-1=0;(3)xn-1+xn-2+…+x+1=(x-Z1)(x-Z2)…(x-Zn-1)=(x-Z1)(x-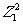 )…(x-
)…(x-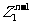 ).
).
6.开方:若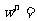 r(cosθ+isinθ),则
r(cosθ+isinθ),则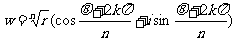 ,k=0,1,2,…,n-1。
,k=0,1,2,…,n-1。
5.棣莫弗定理:[r(cosθ+isinθ)]n=rn(cosnθ+isinnθ).
4.复数的运算法则:(1)按代数形式运算加、减、乘、除运算法则与实数范围内一致,运算结果可以通过乘以共轭复数将分母分为实数;(2)按向量形式,加、减法满足平行四边形和三角形法则;(3)按三角形式,若z1=r1(cosθ1+isinθ1),
z2=r2(cosθ2+isinθ2),则z1••z2=r1r2[cos(θ1+θ2)+isin(θ1+θ2)];若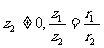 [cos(θ1-θ2)+isin(θ1-θ2)],用指数形式记为z1z2=r1r2ei(θ1+θ2),
[cos(θ1-θ2)+isin(θ1-θ2)],用指数形式记为z1z2=r1r2ei(θ1+θ2),
3. 共轭与模,若z=a+bi,(a,b∈R),则
共轭与模,若z=a+bi,(a,b∈R),则 a-bi称为z的共轭复数。模与共轭的性质有:(1)
a-bi称为z的共轭复数。模与共轭的性质有:(1) ;(2)
;(2) ;(3)
;(3) ;(4)
;(4)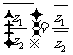 ;(5)
;(5) ;(6)
;(6)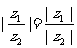 ;(7)||z1|-|z2||≤|z1±z2|≤|z1|+|z2|;(8)|z1+z2|2+|z1-z2|2=2|z1|2+2|z2|2;(9)若|z|=1,则
;(7)||z1|-|z2||≤|z1±z2|≤|z1|+|z2|;(8)|z1+z2|2+|z1-z2|2=2|z1|2+2|z2|2;(9)若|z|=1,则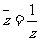 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com