
1.设非零复数a1,a2,a3,a4,a5满足
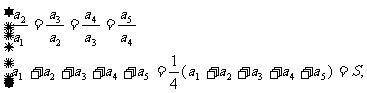
其中S为实数且|S|≤2,求证:复数a1,a2,a3,a4,a5在复平面上所对应的点位于同一圆周上。
13.对于适合|z|≤1的每一个复数z,要使0<|αz+β|<2总能成立,试问:复数α,β应满足什么条件?
12.证明:如果复数A的模为1,那么方程 的所有根都是不相等的实根(n∈N+).
的所有根都是不相等的实根(n∈N+).
11.集合A={z|z18=1},B={w|w48=1},C={zw|z∈A,w∈B},问:集合C中有多少个不同的元素?
10.已知复数z1,z2满足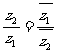 ,且
,且 ,
,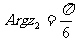 ,
,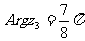 ,则
,则 的值是__________。
的值是__________。
9.当n∈N,且1≤n≤100时,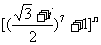 的值中有实数__________个。
的值中有实数__________个。
8.复平面上,非零复数z1,z2在以i为圆心,1为半径的圆上,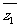 •z2的实部为零,z1的辐角主值为
•z2的实部为零,z1的辐角主值为 ,则z2=__________。
,则z2=__________。
7.已知(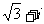 )m=(1+i)n(m,n∈N+),则mn的最小值是__________。
)m=(1+i)n(m,n∈N+),则mn的最小值是__________。
6.设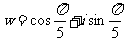 ,则(x-w)(x-w3)(x-w7)(x-w9)的展开式为__________。
,则(x-w)(x-w3)(x-w7)(x-w9)的展开式为__________。
5.设 ,z1=w-z,z2=w+z,z1,z2对应复平面上的点A,B,点O为原点,∠AOB=900,|AO|=|BO|,则ΔOAB面积是__________。
,z1=w-z,z2=w+z,z1,z2对应复平面上的点A,B,点O为原点,∠AOB=900,|AO|=|BO|,则ΔOAB面积是__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com