5．向量法。

例6　 设P是ΔABC所在平面上的一点，G是ΔABC的重心，求证：PA+PB+PC>3PG.

4．三角法。

例5　 设AD，BE与CF为ΔABC的内角平分线，D，E，F在ΔABC的边上，如果∠EDF=90⁰，求∠BAC的所有可能的值。

3．几何变换。

例3　 (蝴蝶定理)AB是⊙O的一条弦，M为AB中点，CD，EF为过M的任意弦，CF，DE分别交AB于P，Q。求证：PM=MQ。

例4　 平面上每一点都以红、蓝两色之一染色，证明：存在这样的两个相似三角形，它们的相似比为1995，而且每个三角形三个顶点同色。

1．同一法。即不直接去证明，而是作出满足条件的图形或点，然后证明它与已知图形或点重合。

例1　 在ΔABC中，∠ABC=70⁰，∠ACB=30⁰，P，Q为ΔABC内部两点，∠QBC=∠QCB=10⁰，∠PBQ=∠PCB=20⁰，求证：A，P，Q三点共线。

2面积法。

例2 ◇ABCD中，E，F分别是CD，BC上的点，且BE=DF，BE交DF于P，求证：AP为∠BPD的平分线。

梅涅劳斯定理　 设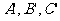分别是ΔABC的三边BC，CA，AB或其延长线上的点，若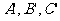三点共线，则

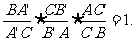
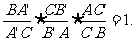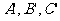梅涅劳斯定理的逆定理　 条件同上，若则三点共线。

塞瓦定理　 设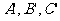分别是ΔABC的三边BC，CA，AB或其延长线上的点，若三线平行或共点，则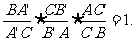

塞瓦定理的逆定理　 设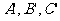分别是ΔABC的三边BC，CA，AB或其延长线上的点，若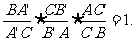则三线共点或互相平行。

角元形式的塞瓦定理　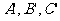 分别是ΔABC的三边BC，CA，AB所在直线上的点，则平行或共点的充要条件是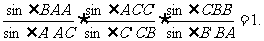

广义托勒密定理　 设ABCD为任意凸四边形，则AB•CD+BC•AD≥AC•BD，当且仅当A，B，C，D四点共圆时取等号。

斯特瓦特定理　 设P为ΔABC的边BC上任意一点，P不同于B，C，则有

AP²=AB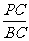²•+AC²•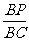-BP•PC.

西姆松定理　 过三角形外接圆上异于三角形顶点的任意一点作三边的垂线，则三垂足共线。

西姆松定理的逆定理　 若一点在三角形三边所在直线上的射影共线，则该点在三角形的外接圆上。

九点圆定理　 三角形三条高的垂足、三边的中点以及垂心与顶点的三条连线段的中点，这九点共圆。

蒙日定理　 三条根轴交于一点或互相平行。(到两圆的幂(即切线长)相等的点构成集合为一条直线，这条直线称根轴)

欧拉定理　 ΔABC的外心O，垂心H，重心G三点共线，且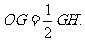

6.设z₁,z₂,z₃为复数，求证：

|z₁|+|z₂|+|z₃|+|z₁+z₂+z₃|≥|z₁+z₂|+|z₂+z₃|+|z₃+z₁|。

5．已知复数z满足11z¹⁰+10iz⁹+10iz-11=0，求证：|z|=1.

4．运用复数证明：任给8个非零实数a₁,a₂,…,a₈，证明六个数a₁a₃+a₂a₄, a₁a₅+a₂a₆, a₁a₇+a₂a₈, a₃a₅+a₄a₆, a₃a₇+a₄a₈,a₅a₇+a₆a₈中至少有一个是非负数。

3．已知p(z)=zⁿ+c₁z^n-1+c₂z^n-2+…+c_n是复变量z的实系数多项式，且|p(i)|<1，求证：存在实数a,b,使得p(a+bi)=0且(a²+b²+1)²<4b²+1.

2．求证：。