8．ΔABC中，∠C=90⁰，∠A=30⁰，BC=1，求ΔABC的内接三角形(三个顶点分别在三条边上的三角形)的最长边的最小值。

7．已知点A₁，B₁，C₁，点A₂，B₂，C₂，分别在直线l₁,l₂上 ，B₂C₁交B₁C₂于点M，C₁A₂交A₁C₂于点N，B₁A₂交B₂A₁于L。求证：M，N，L三点共线。

6．设点I，H分别是锐角ΔABC的内心和垂心，点B₁，C₁分别是边AC，AB的中点，已知射线B₁I交边AB于点B₂(B₂≠B)，射线C₁I交AC的延长线于点C₂，B₂C₂与BC相交于点K，A₁为ΔBHC的外心。试证：A，I，A₁三点共线的充要条件是ΔBKB₂和ΔCKC₂的面积相等。

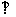5．ΔABC中，O为外心，三条高AD，BE，CF相交于点H，直线ED和AB相交于点M，直线FD和AC相交于点N，求证：(1)OBDF，OC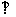DE；(2)OH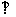MN。

4．ΔABC内有两点M，N，使得∠MAB=∠NAC且∠MBA=∠NBC，求证：

3．已知两小圆⊙O₁与⊙O₂相外切且都与大圆⊙O相内切，AB是⊙O₁与⊙O₂的一条外公切线，A，B在⊙O上，CD是⊙O₁与⊙O₂的内公切线，⊙O₁与⊙O₂相切于点P，且P，C在直线AB的同一侧，求证：P是ΔABC的内心。

2．设⊙O的外切四边形ABCD的对角线AC，BD的中点分别为E，F，求证：E，O，F三点共线。

1．⊙O₁和⊙O₂分别是ΔABC的边AB，AC上的旁切圆，⊙O₁与CB，CA的延长线切于E，G，⊙O₂与BC，BA的延长线切于F，H，直线EG与FH交于点P，求证：PA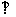BC。

7．四点共圆。

例8　 直线l与⊙O相离，P为l上任意一点，PA，PB为圆的两条切线，A，B为切点，求证：直线AB过定点。

6．解析法。

例7　 H是ΔABC的垂心，P是任意一点，HL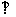PA，交PA于L，交BC于X，HM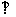PB，交PB于M，交CA于Y，HN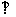PC交PC于N，交AB于Z，求证：X，Y，Z三点共线。