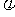10．(欧拉函数值的计算公式)若，则(m)=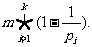

9．若(a,m)=1，则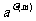≡1(modm),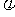(m)称欧拉函数。

8．Fermat小定理：若p为素数，p>a,(a,p)=1，则a^p-1≡1(modp)，且对任意整数a,有a^p≡a(modp).

7．完全剩余系：一组数y₁,y₂,…,y_s满足：对任意整数a有且仅有一个y_j是a对模m的剩余，即a≡y_j(modm)，则y₁,y₂,…,y_s称为模m的完全剩余系。

6．同余：设m≠0,若m|(a-b)，即a-b=km，则称a与b模同m同余，记为a≡b(modm)，也称b是a对模m的剩余。

5．算术基本定理：若n>1且n为整数，则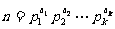，其中p_j(j=1,2,…,k)是质数(或称素数)，且在不计次序的意义下，表示是唯一的。

4．由3可得：(1)u_k+1=(u₀,u₁)；(2)d|u₀且d|u₁的充要条件是d|u_k+1；(3)存在整数x

₀,x₁，使u_k+1=x₀u₀+x₁u₁.

3．辗转相除法：设u₀,u₁是给定的两个整数，u₁≠0，u₁　 u₀,由2可得下面k+1个等式：u₀=q₀u₁+u₂,0<u₂<|u₁|；

u₁=q₁u₂+u₃,0<u₃<u₂；

u₂=q₂u₃+u₄,0<u₄<u₃；

…

u_k-2=q_k-2u₁+u_k-1+u_k,0<u_k<u_k-1；

u_k-1=q_k-1u_k+1,0<u_k+1<u_k；

u_k=q_ku_k+1.

1．整除：设a,b∈Z,a≠0，如果存在q∈Z使得b=aq，那么称b可被a整除，记作a|b，且称b是a的倍数,a是b的约数。b不能被a整除，记作a　 b.

2　 带余数除法：设a,b是两个给定的整数，a≠0，那么，一定存在唯一一对整数q与r，满足b=aq+r,0≤r<|a|，当r=0时a|b。 　

9．ΔABC的垂心为H，外心为O，外接圆半径为R，顶点A，B，C关于对边BC，CA，AB的对称点分别为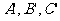，求证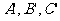：三点共线的充要条件是OH=2R。