2．设a,b,c∈N₊，且a²+b²-abc是不超过c+1的一个正整数，求证：a²+b²-abc是一个完全平方数。

1．试求所有正整数对(a,b)，使得(ab-a²+b+1)|(ab+1).

7．进位制的作用

例7　 能否选择1983个不同的正整数都不大于10⁵，且其中没有3个正整数是等差数列中的连续项？证明你的结论。

6．整除的应用。

例6　 求出所有的有序正整数数对(m,n)，使得是整数。

5．最小数原理。

例5　 证明：方程x⁴+y⁴=z²没有正整数解。

4．特殊模法。

例4　 证明：存在无穷多个正整数，它们不能表示成少于10个奇数的平方和。

3．无穷递降法。

例3　 确定并证明方程a²+b²+c²=a²b²的所有整数解。

2．不等分析法。

例2　 试求所有的正整数n，使方程x³+y³+z³=nx²y²z²有正整数解。

1．奇偶分析法。

例1　 有n个整数，它们的和为0，乘积为n，(n>1)，求证：4|n。

11．(孙子定理)设m₁,m₂,…,m_k是k个两两互质的正整数，则同余组：

x≡b₁(modm₁),x≡b₂(modm₂),…,x≡b_k(modm_k)有唯一解，

x≡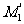M₁b₁+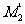M₂b₂+…+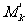M_kb_k(modM)，

其中M=m₁m₂m_k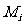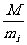；=，i=1,2,…,k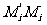；≡1(modm_i),i=1,2,…,k.