
4.构造法。
例5 是否存在一个无穷正整数数列a1,<a2<a3<…,使得对任意整数A,数列 中仅有有限个素数。
中仅有有限个素数。
[证明] 存在。取an=(n!)3即可。当A=0时,{an}中没有素数;当|A|≥2时,若n≥|A|,则an+A均为|A|的倍数且大于|A|,不可能为素数;当A=±1时,an±1=(n!±1)•[(n!)2±n!+1],当≥3时均为合数。从而当A为整数时,{(n!)3+A}中只有有限个素数。
例6 一个多面体共有偶数条棱,试证:可以在它的每条棱上标上一个箭头,使得对每个顶点,指向它的箭头数目是偶数。
[证明] 首先任意给每条棱一个箭头,如果此时对每个顶点,指向它的箭头数均为偶数,则命题成立。若有某个顶点A,指向它的箭头数为奇数,则必存在另一个顶点B,指向它的箭头数也为奇数(因为棱总数为偶数),对于顶点A与B,总有一条由棱组成的“路径”连结它们,对该路径上的每条棱,改变它们箭头的方向,于是对于该路径上除A,B外的每个顶点,指向它的箭头数的奇偶性不变,而对顶点A,B,指向它的箭头数变成了偶数。如果这时仍有顶点,指向它的箭头数为奇数,那么重复上述做法,又可以减少两个这样的顶点,由于多面体顶点数有限,经过有限次调整,总能使和是对每个顶点,指向它的箭头数为偶数。命题成立。
3.不变量原理。
俗话说,变化的是现象,不变的是本质,某一事情反复地进行,寻找不变量是一种策略。
例3 设正整数n是奇数,在黑板上写下数1,2,…,2n,然后取其中任意两个数a,b,擦去这两个数,并写上|a-b|。证明:最后留下的是一个奇数。
[证明] 设S是黑板上所有数的和,开始时和数是S=1+2+…+2n=n(2n+1),这是一个奇数,因为|a-b|与a+b有相同的奇偶性,故整个变化过程中S的奇偶性不变,故最后结果为奇数。
例4 数a1, a2,…,an中每一个是1或-1,并且有S=a1a2a3a4+ a2a3a4a5+…+ana1a2a3=0. 证明:4|n.
[证明] 如果把a1, a2,…,an中任意一个ai换成-ai,因为有4个循环相邻的项都改变符号,S模4并不改变,开始时S=0,即S≡0,即S≡0(mod4)。经有限次变号可将每个ai都变成1,而始终有S≡0(mod4),从而有n≡0(mod4),所以4|n。
1.抽屉原理。
例1 设整数n≥4,a1,a2,…,an是区间(0,2n)内n个不同的整数,证明:存在集合{a1,a2,…,an}的一个子集,它的所有元素之和能被2n整除。
[证明] (1)若n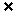 {a1,a2,…,an},则n个不同的数属于n-1个集合{1,2n-1},{2,2n-2},…,{n-1,n+1}。由抽屉原理知其中必存在两个数ai,aj(i≠j)属于同一集合,从而ai+aj=2n被2n整除;
{a1,a2,…,an},则n个不同的数属于n-1个集合{1,2n-1},{2,2n-2},…,{n-1,n+1}。由抽屉原理知其中必存在两个数ai,aj(i≠j)属于同一集合,从而ai+aj=2n被2n整除;
(2)若n∈{a1,a2,…,an},不妨设an=n,从a1,a2,…,an-1(n-1≥3)中任意取3个数ai, aj, ak(ai,<aj< ak),则aj-ai与ak-ai中至少有一个不被n整除,否则ak-ai=(ak-aj)+(aj-ai)≥2n,这与ak∈(0,2n)矛盾,故a1,a2,…,an-1中必有两个数之差不被n整除;不妨设a1与a2之差(a2-a1>0)不被n整除,考虑n个数a1,a2,a1+a2,a1+a2+a3,…,a1+a2+…+an-1。
ⅰ)若这n个数中有一个被n整除,设此数等于kn,若k为偶数,则结论成立;若k为奇数,则加上an=n知结论成立。
ⅱ)若这n个数中没有一个被n整除,则它们除以n的余数只能取1,2,…,n-1这n-1个值,由抽屉原理知其中必有两个数除以n的余数相同,它们之差被n整除,而a2-a1不被n整除,故这个差必为ai, aj, ak-1中若干个数之和,同ⅰ)可知结论成立。
2 极端原理。
极端原理。
例2 在n×n的方格表的每个小方格内写有一个非负整数,并且在某一行和某一列的交叉点处如果写有0,那么该行与该列所填的所有数之和不小于n。证明:表中所有数之和不小于 。
。
[证明] 计算各行的和、各列的和,这2n个和中必有最小的,不妨设第m行的和最小,记和为k,则该行中至少有n-k个0,这n-k个0所在的各列的和都不小于n-k,从而这n-k列的数的总和不小于(n-k)2,其余各列的数的总和不小于k2,从而表中所有数的总和不小于(n-k)2+k2≥
9.设a,b,c,d∈N+,且a>b>c>d,ac+bd=(b+d+a-c)(b+d-a+c)。证明:ab+cd不是素数。
8.设x是一个n位数,问:是否总存在非负整数y≤9和z使得10n+1z+10x+y是一个完全平方数?证明你的结论。
7.对于正整数a,n,定义Fn(a)=q+r,其中q,r为非负整数,a=qn+r且0≤r≤n,求最大正整数A,使得存在正整数n1,n2,…,n6,对任意正整数a≤A,都有 =1,并证明你的结论。
=1,并证明你的结论。
6.求最小的正整数n(≥4),满足从任意n个不同的整数中能选出四个不同的数a,b,c,d使20|(a+b-c-d).
5.求证:存在一个具有如下性质的正整数的集合A,对于任何由无限多个素数组成的集合,存在k≥2及正整数m∈A和n A,使得m和n均为S中k个不同元素的乘积。
A,使得m和n均为S中k个不同元素的乘积。
4.求所有的正整数n,使得存在正整数m,(2n-1)|(m2+9).
3.确定所有的正整数数对(x,y),使得x≤y,且x2+1是y的倍数,y2+1是x的倍数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com