
6.竞赛常用方法与例问题。
定理4 容斥原理;用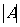 表示集合A的元素个数,则
表示集合A的元素个数,则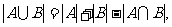
 ,需要xy此结论可以推广到
,需要xy此结论可以推广到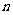 个集合的情况,即
个集合的情况,即
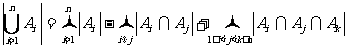

定义8 集合的划分:若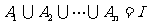 ,且
,且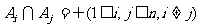 ,则这些子集的全集叫I的一个
,则这些子集的全集叫I的一个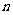 -划分。
-划分。
定理5 最小数原理:自然数集的任何非空子集必有最小数。
定理6 抽屉原理:将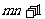 个元素放入
个元素放入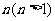 个抽屉,必有一个抽屉放有不少于
个抽屉,必有一个抽屉放有不少于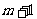 个元素,也必有一个抽屉放有不多于
个元素,也必有一个抽屉放有不多于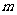 个元素;将无穷多个元素放入
个元素;将无穷多个元素放入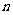 个抽屉必有一个抽屉放有无穷多个元素。
个抽屉必有一个抽屉放有无穷多个元素。
例6 求1,2,3,…,100中不能被2,3,5整除的数的个数。

例7 S是集合{1,2,…,2004}的子集,S中的任意两个数的差不等于4或7,问S中最多含有多少个元素?
例8
求所有自然数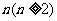 ,使得存在实数
,使得存在实数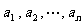 满足:
满足:

例9 设A={1,2,3,4,5,6},B={7,8,9,……,n},在A中取三个数,B中取两个数组成五个元素的集合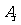 ,
,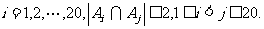 求
求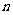 的最小值。
的最小值。
例10 集合{1,2,…,3n}可以划分成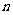 个互不相交的三元集合
个互不相交的三元集合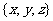 ,其中
,其中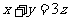 ,求满足条件的最小正整数
,求满足条件的最小正整数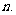
5.配对方法。
例5 给定集合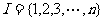 的
的 个子集:
个子集: ,满足任何两个子集的交集非空,并且再添加I的任何一个其他子集后将不再具有该性质,求
,满足任何两个子集的交集非空,并且再添加I的任何一个其他子集后将不再具有该性质,求 的值。
的值。
4.计数原理的应用。
例4 集合A,B,C是I={1,2,3,4,5,6,7,8,9,0}的子集,(1)若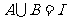 ,求有序集合对(A,B)的个数;(2)求I的非空真子集的个数。
,求有序集合对(A,B)的个数;(2)求I的非空真子集的个数。
3.分类讨论思想的应用。
例3 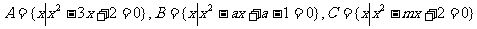 ,若
,若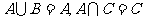 ,求
,求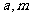
2.利用子集的定义证明集合相等,先证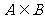 ,再证
,再证 ,则A=B。
,则A=B。
例2 设A,B是两个集合,又设集合M满足
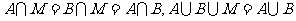 ,求集合M(用A,B表示)。
,求集合M(用A,B表示)。
1.利用集合中元素的属性,检验元素是否属于集合。
例1 设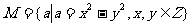 ,求证:
,求证:
(1)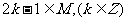 ;
;
(2)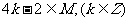 ;
;
(3)若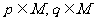 ,则
,则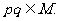
定义1 一般地,一组确定的、互异的、无序的对象的全体构成集合,简称集,用大写字母来表示;集合中的各个对象称为元素,用小写字母来表示,元素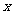 在集合A中,称
在集合A中,称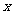 属于A,记为
属于A,记为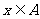 ,否则称
,否则称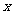 不属于A,记作
不属于A,记作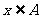 。例如,通常用N,Z,Q,B,Q+分别表示自然数集、整数集、有理数集、实数集、正有理数集,不含任何元素的集合称为空集,用
。例如,通常用N,Z,Q,B,Q+分别表示自然数集、整数集、有理数集、实数集、正有理数集,不含任何元素的集合称为空集,用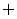 来表示。集合分有限集和无限集两种
来表示。集合分有限集和无限集两种
集合的表示方法有列举法:将集合中的元素一一列举出来写在大括号内并用逗号隔开表示集合的方法,如{1,2,3};描述法:将集合中的元素的属性写在大括号内表示集合的方法。例如{有理数},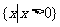 分别表示有理数集和正实数集。
分别表示有理数集和正实数集。
定义2 子集:对于两个集合A与B,如果集合A中的任何一个元素都是集合B中的元素,则A叫做B的子集,记为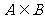 ,例如
,例如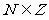 。规定空集是任何集合的子集,如果A是B的子集,B也是A的子集,则称A与B相等。如果A是B的子集,而且B中存在元素不属于A,则A叫B的真子集。
。规定空集是任何集合的子集,如果A是B的子集,B也是A的子集,则称A与B相等。如果A是B的子集,而且B中存在元素不属于A,则A叫B的真子集。
定义3 交集,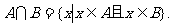
定义4 并集,
定义5 补集,若 称为A在I中的补集。
称为A在I中的补集。
定义6 差集,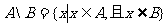 。
。
定义7 集合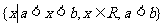 记作开区间
记作开区间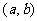 ,集合
,集合
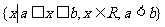 记作闭区间
记作闭区间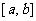 ,R记作
,R记作
定理1 集合的性质:对任意集合A,B,C,有:
(1)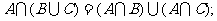 (2)
(2)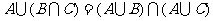 ;
;
(3)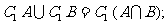 (4)
(4)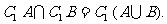
[证明]这里仅证(1)、(3),其余由读者自己完成。
(1)若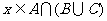 ,则
,则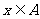 ,且
,且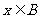 或
或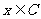 ,所以
,所以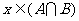 或
或 ,即
,即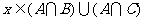 ;反之,
;反之,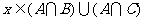 ,则
,则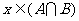 或
或 ,即
,即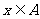 且
且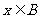 或
或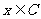 ,即
,即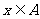 且
且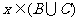 ,即
,即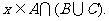
(3)若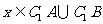 ,则
,则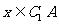 或
或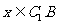 ,所以
,所以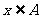 或
或 ,所以
,所以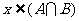 ,又
,又 ,所以
,所以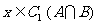 ,即
,即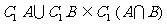 ,反之也有
,反之也有
定理2 加法原理:做一件事有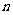 类办法,第一类办法中有
类办法,第一类办法中有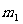 种不同的方法,第二类办法中有
种不同的方法,第二类办法中有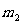 种不同的方法,…,第
种不同的方法,…,第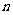 类办法中有
类办法中有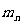 种不同的方法,那么完成这件事一共有
种不同的方法,那么完成这件事一共有 种不同的方法。
种不同的方法。
定理3 乘法原理:做一件事分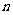 个步骤,第一步有
个步骤,第一步有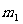 种不同的方法,第二步有
种不同的方法,第二步有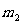 种不同的方法,…,第
种不同的方法,…,第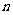 步有
步有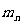 种不同的方法,那么完成这件事一共有
种不同的方法,那么完成这件事一共有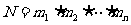 种不同的方法。
种不同的方法。
9.某班共有30名学生,每名学生在班内都有同样多的朋友,期末时任何两人的成绩都可分出优劣,没有相同的。问:比自己的多半朋友的成绩都要好的学生最多能有多少人?
8.设有30个人坐在一张圆桌的周围,其中的每个人都或者是白痴,或者是聪明人。对在座的每个人都提问:“你右边的邻座是聪明人还是白痴?”聪明人总是给出正确的答案,而白痴既可能回答正确,也可能回答不正确。已知白痴的个数不超过F,求总可以指出一位聪明人的最大的F。
7. 设m, n, k∈N,有4个酒杯,容量分别为m,n,k和m+n+k升,允许进行如下操作:将一个杯中的酒倒入另一杯中或者将另一杯倒满为止。开始时,大杯中装满酒而另3个杯子却空着,问:为使对任何S∈N,S<m+n+k,都可经过若干次操作,使得某个杯子中恰有S升酒的关于m,n,k的充分必要条件是什么?
设m, n, k∈N,有4个酒杯,容量分别为m,n,k和m+n+k升,允许进行如下操作:将一个杯中的酒倒入另一杯中或者将另一杯倒满为止。开始时,大杯中装满酒而另3个杯子却空着,问:为使对任何S∈N,S<m+n+k,都可经过若干次操作,使得某个杯子中恰有S升酒的关于m,n,k的充分必要条件是什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com