
5.设S是由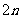 个人组成的集合。求证:其中必定有两个人,他们的公共朋友的个数为偶数。
个人组成的集合。求证:其中必定有两个人,他们的公共朋友的个数为偶数。
4.设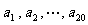 是20个两两不同的整数,且整合
是20个两两不同的整数,且整合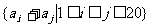 中有201个不同的元素,求集合
中有201个不同的元素,求集合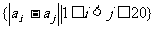 中不同元素个数的最小可能值。
中不同元素个数的最小可能值。
3.某人写了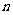 封信,同时写了
封信,同时写了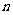 个信封,然后将信任意装入信封,问:每封信都装错的情况有多少种?
个信封,然后将信任意装入信封,问:每封信都装错的情况有多少种?
2.求证:集合{1,2,…,1989}可以划分为117个互不相交的子集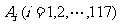 ,使得(1)每个
,使得(1)每个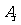 恰有17个元素;(2)每个
恰有17个元素;(2)每个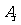 中各元素之和相同。
中各元素之和相同。
1. 是三个非空整数集,已知对于1,2,3的任意一个排列
是三个非空整数集,已知对于1,2,3的任意一个排列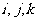 ,如果
,如果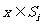 ,
,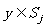 ,则
,则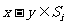 。求证:
。求证: 中必有两个相等。
中必有两个相等。
12.集合S={1,2,3,4,5,6,7,8,9,0}的若干个五元子集满足:S中的任何两个元素至多出现在两个不同的五元子集中,问:至多有多少个五元子集?
11.S是Q的子集且满足:若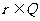 ,则
,则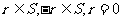 恰有一个成立,并且若
恰有一个成立,并且若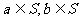 ,则
,则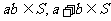 ,试确定集合S。
,试确定集合S。
10.求集合B和C,使得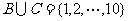 ,并且C的元素乘积等于B的元素和。
,并且C的元素乘积等于B的元素和。
9.已知集合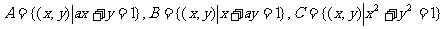 ,问:当
,问:当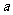 取何值时,
取何值时,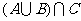 为恰有2个元素的集合?说明理由,若改为3个元素集合,结论如何?
为恰有2个元素的集合?说明理由,若改为3个元素集合,结论如何?
8.已知集合A,B,aC(不必相异)的并集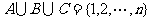 , 则满足条件的有序三元组(A,B,C)个数是___________。
, 则满足条件的有序三元组(A,B,C)个数是___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com