
4. 不等式ax2+(ab+1)x+b>0的解是1<x<2,则a, b的值是____________.
3. 当|x-2|<a时,不等式|x2-4|<1成立,则正数a的取值范围是________.
2.由上列各组命题构成“p或q”,“p且q”,“非p”形式的复合命题中,p或q为真,p且q为假,非p为真的是_________.①p;3是偶数,q:4是奇数;②p:3+2=6,q:③p:a∈(a,b),q:{a} {a,b}; ④
p: Q
{a,b}; ④
p: Q R, q: N=Z.
R, q: N=Z.
1.下列四个命题中属于真命题的是________,①“若x+y=0,则x、y互为相反数”的逆命题;②“两个全等三角形的面积相等”的否命题;③“若q≤1,则x2+x+q=0有实根”的逆否命题;④“不等边三角形的三个内角相等”的逆否命题。
9.常用结论。
定理1 若a, b∈R, |a|-|b|≤|a+b|≤|a|+|b|.
[证明] 因为-|a|≤a≤|a|,-|b|≤b≤|b|,所以-(|a|+|b|)≤a+b≤|a|+|b|,
所以|a+b|≤|a|+|b|(注:若m>0,则-m≤x≤m等价于|x|≤m).
又|a|=|a+b-b|≤|a+b|+|-b|,
即|a|-|b|≤|a+b|.综上定理1得证。
定理2 若a,b∈R, 则a2+b2≥2ab;若x,y∈R+,则x+y≥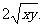
(证略)
注 定理2可以推广到n个正数的情况,在不等式证明一章中详细论证。
8.充分性与必要性。
例9 设定数A,B,C使得不等式
A(x-y)(x-z)+B(y-z)(y-x)+C(z-x)(z-y)≥0 ①
对一切实数x,y,z都成立,问A,B,C应满足怎样的条件?(要求写出充分必要条件,而且限定用只涉及A,B,C的等式或不等式表示条件)
7.一元二次不等式问题的解法。
例8 已知不等式组 ①②的整数解恰好有两个,求a的取值范围。
①②的整数解恰好有两个,求a的取值范围。
6.定义在区间上的二次函数的最值。
例6 当x取何值时,函数y=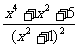 取最小值?求出这个最小值。
取最小值?求出这个最小值。
例7 设变量x满足x2+bx≤-x(b<-1),并且x2+bx的最小值是 ,求b的值。
,求b的值。
5.构造二次函数解题。
例5 已知关于x的方程(ax+1)2=a2(a-x2), a>1,求证:方程的正根比1小,负根比-1大。
4.利用二次函数表达式解题。
例4 设二次函数f(x)=ax2+bx+c(a>0),方程f(x)=x的两根x1, x2满足0<x1<x2<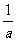 ,
,
(Ⅰ)当x∈(0, x1)时,求证:x<f(x)<x1;
(Ⅱ)设函数f(x)的图象关于x=x0对称,求证:x0<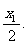
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com