定义1　 映射，对于任意两个集合A，B，依对应法则f，若对A中的任意一个元素x，在B中都有唯一一个元素与之对应，则称f: A→B为一个映射。

定义2　 单射，若f: A→B是一个映射且对任意x, y∈A, x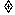y, 都有f(x)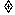f(y)则称之为单射。

定义3　 满射，若f: A→B是映射且对任意y∈B，都有一个x∈A使得f(x)=y，则称f: A→B是A到B上的满射。

定义4　 一一映射，若f: A→B既是单射又是满射，则叫做一一映射，只有一一映射存在逆映射，即从B到A由相反的对应法则f^-1构成的映射，记作f^-1: A→B。

定义5　 函数，映射f: A→B中，若A，B都是非空数集，则这个映射为函数。A称为它的定义域，若x∈A, y∈B，且f(x)=y(即x对应B中的y)，则y叫做x的象，x叫y的原象。集合{f(x)|x∈A}叫函数的值域。通常函数由解析式给出，此时函数定义域就是使解析式有意义的未知数的取值范围，如函数y=3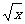-1的定义域为{x|x≥0,x∈R}.

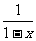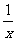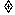　定义6　 反函数，若函数f: A→B(通常记作y=f(x))是一一映射，则它的逆映射f^-1: A→B叫原函数的反函数，通常写作y=f^-1(x). 这里求反函数的过程是：在解析式y=f(x)中反解x得x=f^-1(y)，然后将x, y互换得y=f^-1(x)，最后指出反函数的定义　 域即原函数的值域。例如：函数y=的反函数是y=1-(x0).

定理1　 互为反函数的两个函数的图象关于直线y=x对称。

定理2　 在定义域上为增(减)函数的函数，其反函数必为增(减)函数。

定义7　 函数的性质。

(1)单调性：设函数f(x)在区间I上满足对任意的x₁, x₂∈I并且x₁< x₂，总有f(x₁)<f(x₂)(f(x_­)>f(x₂))，则称f(x)在区间I上是增(减)函数，区间I称为单调增(减)区间。

(2)奇偶性：设函数y=f(x)的定义域为D，且D是关于原点对称的数集，若对于任意的x∈D，都有f(-x)=-f(x)，则称f(x)是奇函数；若对任意的x∈D，都有f(-x)=f(x)，则称f(x)是偶函数。奇函数的图象关于原点对称，偶函数的图象关于y轴对称。

(3)周期性：对于函数f(x)，如果存在一个不为零的常数T，使得当x取定义域内每一个数时，f(x+T)=f(x)总成立，则称f(x)为周期函数，T称为这个函数的周期，如果周期中存在最小的正数T₀，则这个正数叫做函数f(x)的最小正周期。

定义8　 如果实数a<b，则数集{x|a<x<b, x∈R}叫做开区间，记作(a,b)，集合{x|a≤x≤b,x∈R}记作闭区间[a,b]，集合{x|a<x≤b}记作半开半闭区间(a,b]，集合{x|a≤x<b}记作半闭半开区间[a, b)，集合{x|x>a}记作开区间(a, +∞)，集合{x|x≤a}记作半开半闭区间(-∞,a].

定义9　 函数的图象，点集{(x,y)|y=f(x), x∈D}称为函数y=f(x)的图象，其中D为f(x)的定义域。通过画图不难得出函数y=f(x)的图象与其他函数图象之间的关系(a,b>0)；(1)向右平移a个单位得到y=f(x-a)的图象；(2)向左平移a个单位得到y=f(x+a)的图象；(3)向下平移b个单位得到y=f(x)-b的图象；(4)与函数y=f(-x)的图象关于y轴对称；(5)与函数y=-f(-x)的图象关于原点成中心对称；(6)与函数y=f^-1(x)的图象关于直线y=x对称；(7)与函数y=-f(x)的图象关于x轴对称。

定理3　 复合函数y=f[g(x)]的单调性，记住四个字：“同增异减”。例如y=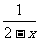, u=2-x在(-∞,2)上是减函数，y=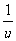在(0，+∞)上是减函数，所以y=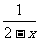在(-∞,2)上是增函数。

注：复合函数单调性的判断方法为同增异减。这里不做严格论证，求导之后是显然的。

9．设a,b,c为实数，g(x)=ax²+bx+c, |x|≤1，求使下列条件同时满足的a, b, c的值：

(ⅰ)=381;

(ⅱ)g(x)_max=444;

(ⅲ)g(x)_min=364.

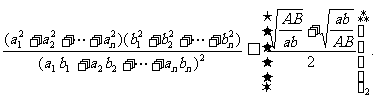
8．设a,b,A,B∈R⁺, a<A, b<B，若n个正数a₁, a₂,…,a_n位于a与A之间，n个正数b₁, b₂,…,b_n位于b与B之间，求证：

7.求证：方程3ax²+2bx-(a+b)=0(b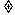0)在(0,1)内至少有一个实根。

6．设二次函数f(x)=ax²+bx+c (a,b,c∈R, a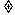0)满足下列条件：

1)当x∈R时，f(x-4)=f(2-x)，且f(x)≥x；

2)当x∈(0, 2)时，f(x)≤;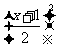

3)f(x)在R上最小值为0。

求最大的m(m>1)，使得存在t∈R，只要x∈[1, m]就有f(x+t)≤x.

5．已知f(x)=x²+ax+b，若存在实数m，使得|f(m)|≤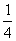,|f(m+1)|≤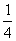,求△=a²-4b的最大值和最小值。

4．F(x)=ax²+bx+c，a,b,c∈R, 且|F(0)|≤1,|F(1)|≤1,|F(-1)|≤1,则对于|x|≤1，求|F(x)|的最大值。

3．设x₁,x₂,…,x_n∈[a, a+1]，且设x=, y=, 求f=y-x²的最大值。

2．设函数f(x)=ax²+8x+3(a<0)，对于给定的负数a，有一个最大的正数l(a)，使得在整个区间[0，l(a)]上，不等式|f(x)|≤5都成立。求l(a)的最大值及相应a的值。

1．设f(x)=ax²+bx+c，a,b,c∈R, a>100，试问满足|f(x)|≤50的整数x最多有几个？