3．对数函数及其性质：形如y=log_ax(a>0, a1)的函数叫做对数函数，其定义域为(0，+∞)，值域为R，图象过定点(1，0)。当0<a<1，y=log_ax为减函数，当a>1时，y=log_ax为增函数。

1．指数函数及其性质：形如y=a^x(a>0, a1)的函数叫做指数函数，其定义域为R，值域为(0，+∞)，当0<a<1时，y=a^x是减函数，当a>1时，y=a^x为增函数，它的图象恒过定点(0，1)。

2 分数指数幂：。

9．设Q⁺是正有理数的集合，试构造一个函数f: Q⁺→Q⁺，满足这样的条件：f(xf(y))=x, y∈Q⁺. 　

8．函数y=f(x)定义在整个实轴上，它的图象在围绕坐标原点旋转角后不变。(1)求证：方程f(x)=x恰有一个解；(2)试给出一个具有上述性质的函数。

7．函数f(x)定义在整数集上，且满足f(n)=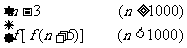，求f(100)的值。

6．已知f: (0,1)→R且f(x)=.

当x∈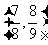时，试求f(x)的最大值。

5．对给定的正数p,q∈(0, 1)，有p+q>1≥p²+q²，试求f(x)=(1-x)+在[1-q,p]上的最大值。

4. 试求f(x,y)=6(x²+y²)(x+y)-4(x²+xy+y²)-3(x+y)+5(x>0, y>0)的最小值。

3. f:[0,1]→R满足：(1)任意x∈[0, 1], f(x)≥0；(2)f(1)=1；(3)当x, y, x+y∈[0, 1]时，f(x)+f(y)≤f(x+y)，试求最小常数c，对满足(1)，(2)，(3)的函数f(x)都有f(x)≤cx.

2.设f(x)对一切x>0有定义，且满足：(ⅰ)f(x)在(0，+∞)是增函数；(ⅱ)任意x>0, f(x)f=1，试求f(1).