
5.命题p: 函数y=log2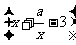 在[2,+∞)上是增函数;命题q: 函数y=log2(ax2-4x+1)的值域为R,则p是q的_________条件。
在[2,+∞)上是增函数;命题q: 函数y=log2(ax2-4x+1)的值域为R,则p是q的_________条件。
4.若log2a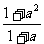 <0,则a 取值范围是_________。
<0,则a 取值范围是_________。
3.已知f(x)是定义在R上的增函数,点A(-1,1),B(1,3)在它的图象上,y=f-1(x)是它的反函数,则不等式|f-1(log2x)|<1的解集为_________。
2.如果x1是方程x+lgx=27的根,x2是方程x+10x=27的根,则x1+x2=_________.
1.命题p: “(log23)x-(log53)x≥(log23)-y-(log53)-y”是命题q:“x+y≥0”的_________条件。
2.指数和对数的运算技巧。
例4 设p, q∈R+且满足log9p= log12q= log16(p+q),求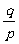 的值。
的值。
例5 对于正整数a, b,
c(a≤b≤c)和实数x, y,
z, w,若ax=by=cz=70w,且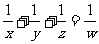 ,求证:a+b=c.
,求证:a+b=c.
例6 已知x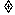 1, ac
1, ac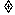 1, a
1, a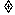 1, c
1, c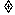 1. 且logax+logcx=2logbx,求证c2=(ac)logab.
1. 且logax+logcx=2logbx,求证c2=(ac)logab.
例7 解方程:3x+4 x +5 x =6 x.
例8 解方程组: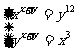 (其中x, y∈R+).
(其中x, y∈R+).
例9 已知a>0, a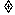 1,试求使方程loga(x-ak)=loga2(x2-a2)有解的k的取值范围。
1,试求使方程loga(x-ak)=loga2(x2-a2)有解的k的取值范围。
1.构造函数解题。
例1 已知a, b, c∈(-1, 1),求证:ab+bc+ca+1>0.
例2 (柯西不等式)若a1, a2,…,an是不全为0的实数,b1, b2,…,bn∈R,则(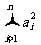 )·(
)·(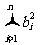 )≥(
)≥(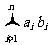 )2,等号当且仅当存在
)2,等号当且仅当存在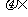 R,使ai=
R,使ai=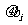 , i=1, 2, …, n时成立。
, i=1, 2, …, n时成立。
例3 设x, y∈R+, x+y=c,
c为常数且c∈(0, 2],求u=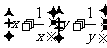 的最小值。
的最小值。
6.连续函数的性质:若a<b, f(x)在[a, b]上连续,且f(a)·f(b)<0,
则f(x)=0在(a,b)上至少有一个实根。
5. 函数y=x+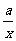 (a>0)的单调递增区间是
(a>0)的单调递增区间是 和
和 ,单调递减区间为
,单调递减区间为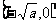 和
和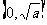 。(请读者自己用定义证明)
。(请读者自己用定义证明)
4.对数的性质(M>0, N>0);
1)ax=M x=logaM(a>0, a
x=logaM(a>0, a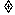 1);
1);
2)loga(MN)= loga M+ loga N;
3)loga(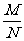 )= loga M- loga N;4)loga Mn=n loga M;,
)= loga M- loga N;4)loga Mn=n loga M;,
5)loga  =
=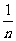 loga M;6)aloga M=M; 7) loga b=
loga M;6)aloga M=M; 7) loga b=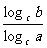 (a,b,c>0,
a, c
(a,b,c>0,
a, c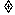 1).
1).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com