4. 等差数列{a_n}满足3a₈=5a₁₃，且a₁>0, S_n为前n项之和，则当S_n最大时，n=_________.

3. 数列{x_n}满足x₁=1，x_n=+2n-1(n≥2)，则{x_n}的通项x_n=_________.

2. 数列{x_n}满足x₁=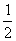，x_n+1=,则{x_n}的通项x_n=_________.

1． 数列{x_n}满足x₁=2, x_n+1=S_n+(n+1)，其中S_n为{x_n}前n项和，当n≥2时，x_n=_________.

5．构造等差或等比数列。

例11　 正数列a₀,a₁,…,a_n,…满足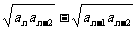=2a_n-1(n≥2)且a₀=a₁=1，求通项。

例12　 已知数列{x_n}满足x₁=2, x_n+1=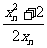,n∈N₊, 求通项。

4．特征方程法。

例9　 已知数列{a_n}满足a₁=3, a₂=6, a_n+2=4_n+1-4a_n，求a_n.

例10　 已知数列{a_n}满足a₁=3, a₂=6, a_n+2=2a_n+1+3a_n，求通项a_n.

3．数列求和法。

数列求和法主要有倒写相加、裂项求和法、错项相消法等。

例6　 已知a_n=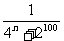(n=1, 2, …)，求S₉₉=a₁+a₂+…+a₉₉.

例7　 求和：+…+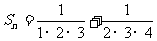

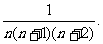
例8　 已知数列{a_n}满足a₁=a₂=1，a_n+2=a_n+1+a_n, S_n为数列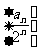的前n项和，求证：S_n<2。

1．不完全归纳法。

这种方法是从特殊情况出发去总结更一般的规律，当然结论未必都是正确的，但却是人类探索未知世界的普遍方式。通常解题方式为：特殊→猜想→数学归纳法证明。

例1　 试给出以下几个数列的通项(不要求证明)；1)0，3，8，15，24，35，…；2)1，5，19，65，…；3)-1，0，3，8，15，…。

例2　 已知数列{a_n}满足a₁=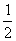,a₁+a_­2+…+a_n=n²a_n, n≥1，求通项a_n.

例3　 设0<a<1，数列{a_n}满足a_n=1+a, a_n-1=a+，求证：对任意n∈N₊,有a_n>1.

2迭代法。

数列的通项a_n或前n项和S_n中的n通常是对任意n∈N成立，因此可将其中的n换成n+1或n-1等，这种办法通常称迭代或递推。

例4　 数列{a_n}满足a_n+pa_n-1+qa_n-2=0, n≥3，q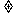0，求证：存在常数c，使得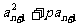·a_n+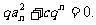

例5　 已知a₁=0, a_n+1=5a_n+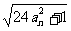，求证：a_n都是整数，n∈N₊.

定义1　 数列，按顺序给出的一列数，例如1，2，3，…，n，…. 数列分有穷数列和无穷数列两种，数列{a_n}的一般形式通常记作a₁, a₂, a₃,…，a_n或a₁, a₂, a₃,…，a_n…。其中a₁叫做数列的首项，a_n是关于n的具体表达式，称为数列的通项。

定理1　 若S_n表示{a_n}的前n项和，则S₁=a₁, 当n>1时，a_n=S_n-S_n-1.

定义2　 等差数列，如果对任意的正整数n，都有a_n+1-a_n=d(常数)，则{a_n}称为等差数列，d叫做公差。若三个数a, b, c成等差数列，即2b=a+c，则称b为a和c的等差中项，若公差为d, 则a=b-d, c=b+d.

定理2　 等差数列的性质：1)通项公式a_n=a₁+(n-1)d；2)前n项和公式：S_n=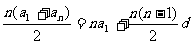；3)a_n-a_m=(n-m)d，其中n, m为正整数；4)若n+m=p+q，则a_n+a_m=a_p+a­_q；5)对任意正整数p, q，恒有a_p-a_q=(p-q)(a₂-a₁)；6)若A，B至少有一个不为零，则{a_n}是等差数列的充要条件是Sn=An²+Bn.

定义3　 等比数列，若对任意的正整数n，都有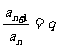，则{a_n}称为等比数列，q叫做公比。

定理3　 等比数列的性质：1)a_n=a₁q^n-1；2)前n项和S_n，当q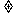1时，S_n=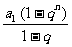；当q=1时，S_n=na₁；3)如果a, b, c成等比数列，即b²=ac(b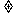0)，则b叫做a, c的等比中项；4)若m+n=p+q，则a_ma_n=a_pa_q。

定义4　 极限，给定数列{a_n}和实数A，若对任意的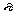>0，存在M，对任意的n>M(n∈N),都有|a_n-A|<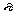，则称A为n→+∞时数列{a_n}的极限，记作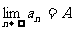

定义5　 无穷递缩等比数列，若等比数列{a_n}的公比q满足|q|<1，则称之为无穷递增等比数列，其前n项和S_n的极限(即其所有项的和)为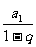(由极限的定义可得)。

定理3　 第一数学归纳法：给定命题p(n)，若：(1)p(n₀)成立；(2)当p(n)时n=k成立时能推出p(n)对n=k+1成立，则由(1)，(2)可得命题p(n)对一切自然数n≥n₀成立。

竞赛常用定理

定理4　 第二数学归纳法：给定命题p(n)，若：(1)p(n₀)成立；(2)当p(n)对一切n≤k的自然数n都成立时(k≥n₀)可推出p(k+1)成立，则由(1)，(2)可得命题p(n)对一切自然数n≥n₀成立。

定理5　 对于齐次二阶线性递归数列x_n=ax_n-1+bx_n-2，设它的特征方程x²=ax+b的两个根为α,β:(1)若α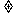β，则x_n=c₁a^n-1+c₂β^n-1，其中c₁, c₂由初始条件x₁, x₂的值确定；(2)若α=β，则x_n=(c₁n+c₂) α^n-1，其中c₁, c₂的值由x₁, x₂的值确定。

9．设α，β为实数，求所有f: R⁺→R，使得对任意的x,y∈R⁺, f(x)f(y)=y²·f成立。