9．设h∈N₊，数列{a_n}定义为：a₀=1, a_n+1=。问：对于怎样的h，存在大于0的整数n，使得a_n=1？

8. 数列{a_n} 称为等差比数列，当且仅当此数列满足a₀=0, {a_n+1-qa_n}构成公比为q的等比数列，q称为此等差比数列的差比。那么，由100以内的自然数构成等差比数列而差比大于1时，项数最多有__________项.

7. 数列{a_n}满足a₁=2, a₂=6, 且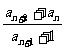=2，则

________.

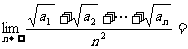6. 各项均为实数的等差数列的公差为4，其首项的平方与其余各项之和不超过100，这样的数列至多有__________项.

5. 等比数列a+log₂3, a+log₄3, a+log₈3的公比为=__________.

4. 已知数列a₀, a₁, a₂, …, a_n, …满足关系式(3-a_n+1)·(6+a_n)=18，且a₀=3，则=__________.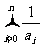

3. 设数列{a_n}满足a₁=3, a_n>0，且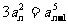，则通项a_n=__________.

2．设数列{x_n}满足x₁=1, x_n=，则通项x_n=__________.

1．设等差数列的首项及公差均为非负整数，项数不少于3，且各项和为97²，这样的数列共有_________个。

13．是否存在常数a, b, c，使题设等式

1·2²+2·3²+…+n·(n+1)²=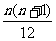(an²+bn+c)

对于一切自然数n都成立？证明你的结论。