8．求证：存在无穷有界数列{x_n}，使得对任何不同的m, k，有|x_m-x_k|≥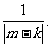

7．整数列u₀,u₁,u₂,u₃,…满足u₀=1，且对每个正整数n, u_n+1u_n-1=ku_u，这里k是某个固定的正整数。如果u₂₀₀₀=2000，求k的所有可能的值。

6．设a₁=a₂=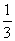，且当n=3,4,5,…时，a_n=,

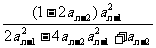(ⅰ)求数列{a_n}的通项公式；(ⅱ)求证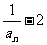：是整数的平方。

5．设x₁,x₂,…,x_n是各项都不大于M的正整数序列且满足x_k=|x_k-1-x_k-2|(k=3,4,…,n)①.试问这样的序列最多有多少项？

4．无穷正实数数列{x_n}具有以下性质：x₀=1，x_i+1<x_i (i=0,1,2,…),

(1)求证：对具有上述性质的任一数列，总能找到一个n≥1，使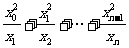≥3.999均成立；

(2)寻求这样的一个数列使不等式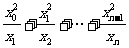<4对任一n均成立。

3．设数列{a_n}和{b_n}满足a₀=1,b₀=0，且

求证：a_n (n=0,1,2,…)是完全平方数。

2．设a₁, a₂,…, a_n表示整数1，2，…，n的任一排列，f(n)是这些排列中满足如下性质的排列数目：①a₁=1; ②|a_i-a_i+1|≤2, i=1,2,…,n-1。

试问f(2007)能否被3整除？

1．设a_n为下述自然数N的个数：N的各位数字之和为n且每位数字只能取1，3或4，求证：a_2n是完全平方数，这里n=1, 2,….

11．求证：存在唯一的正整数数列a₁,a₂,…,使得

a₁=1, a₂>1, a_n+1(a_n+1-1)=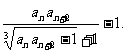

10．设{a_k}_k≥1为一非负整数列，且对任意k≥1，满足a_k≥a_2k+a_2k+1，(1)求证：对任意正整数n，数列中存在n个连续项为0；(2)求出一个满足以上条件，且其存在无限个非零项的数列。